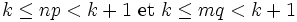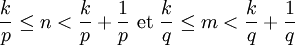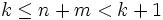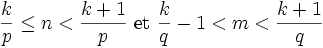Théorème de beatty

Théorème de Beatty

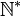Le théorème de Beatty est un théorème d'arithmétique publié en 1926 par le mathématicien canadien Samuel Beatty qui donne une condition nécessaire et suffisante pour que deux suites pseudo-arithmétiques partitionnent $\mathbb{N}^*$ .

Énoncé

Il affirme l'équivalence des deux points suivants :

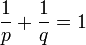
Les nombres p et q sont positifs, irrationnels et vérifient $\frac{1}{p} + \frac{1}{q} = 1$
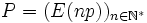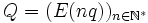Les deux suites d'entiers $P = (E(np))_{n \in \mathbb{N}^*}$ et $Q = (E(nq))_{n \in \mathbb{N}^*}$ forment une partition de l'ensemble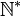 $\mathbb{N}^*$

Ici, la fonction E désigne la fonction partie entière. Ce résultat ne se généralise malheureusement pas : il est impossible de partitionner 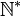$\mathbb{N}^*$ avec plus de trois suites pseudo-arithmétiques.

Démonstration

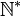
On se donne p et q deux réels strictement positifs, tels que les suites P et Q forment une partition de $\mathbb{N}^*$

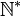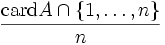Le résultat devient assez intuitif si l'on introduit la densité d'une partie A de $\mathbb{N}^*$ , c'est la limite - si elle existe - lorsque n tend vers $+ \infty$ de $\frac{\textrm{card}A \cap \{1, \dots, n\}}{n}$ . Par exemple, l'ensemble de nombres pairs (ou l'ensemble des nombres impairs) a une densité qui est 1/2, l'ensemble des nombres premiers a comme densité 0.

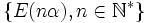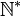On voit facilement que les ensembles $\{E(n\alpha), n \in \mathbb{N}^*\}$ où $α$ est un réel positif ont comme densité $\frac{1}{\alpha}$ . Les supports des suites P et Q forment une partition de $\mathbb{N}^*$ , donc la somme de leurs densités vaut 1 :

$\frac{1}{p} + \frac{1}{q} = 1$

De plus, p et q ne peuvent être tous les deux rationnels, car si c'est le cas 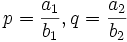$p = \frac{a_1}{b_1}, q = \frac{a_2}{b_2}$ , alors $E (b 1 a 2 p) = E (b 2 a 1 q)( = a 1 a 2)$ . Or les suites P et Q n'ont aucun élément en commun. L'un des deux est irrationnels, et par suite les deux sont irrationnels (car $p - 1 + q - 1 = 1$ )

Réciproquement, si p et q sont irrationnels et $p - 1 + q - 1 = 1$ , montrons par l'absurde que les supports des suites P et Q sont disjoints. Soit k un entier qui s'écrit sous la forme $k = E (n p) = E (m q)$ .

Par définition de la partie entière, nous avons les inégalités suivantes :

$k \leq np < k + 1 \mbox{ et } k \leq mq < k + 1$

Divisons la première inégalité par p, et la seconde par q :

$\frac{k}{p} \leq n < \frac{k}{p} + \frac{1}{p} \mbox{ et } \frac{k}{q} \leq m < \frac{k}{q} + \frac{1}{q}$

Sommons ces deux inégalités, on obtient :

$k \leq n + m < k + 1$

k, n et m étant des entiers, ceci impose que $k = n + m$ . On a forcément égalité dans les deux inégalités précédentes. Donc k = np et k = mq. Ceci est absurde car p et q sont irrationnels.

Montrons maintenant que tout entier naturel non nul est atteint par l'une des deux suites. Soit 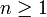$n \geq 1$ et k = E(np). k est atteint par la suite P, donc pas par la suite Q, il existe un unique entier m tel que :

E (m q) < k < E ((m + 1) q)

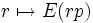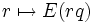En fait, l'entier E(mq) est le plus grand entier de la suite Q inférieur à k. Les applications $r \mapsto E(rp)$ et $r \mapsto E(rq)$ sont injectives car p et q sont plus grands que 1. L'intervalle 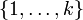$\{1, \dots, k\}$ contient donc $m + n$ éléments des suites P et Q (car ces deux suites ont des supports disjoints). Il suffit de conclure en prouvant k = n + m. On a :

$\frac{k}{p} \leq n < \frac{k + 1}{p} \mbox{ et } \frac{k}{q} - 1 < m < \frac{k+1}{q}$

En additionnant il vient k - 1 < n + m < k + 1, soit k = n + m. CQFD.

Référence

Exercices de mathématiques, oraux X-ENS. Algèbre 1. Serge Francinou, Hervé Gianella, Serge Nicolas. Éditions Cassini.

Voir aussi

Pages contenant des applets pour calculer les termes de la suite de Beatty, ou pour déterminer p et q en fonction des termes de la suite.

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Beatty ».

Catégories : Théorème de mathématiques | Arithmétique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de beatty de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Theoreme de Beatty — Théorème de Beatty Le théorème de Beatty est un théorème d arithmétique publié en 1926 par le mathématicien canadien Samuel Beatty qui donne une condition nécessaire et suffisante pour que deux suites pseudo arithmétiques partitionnent . Énoncé… … Wikipédia en Français
Théorème de Beatty — Le théorème de Beatty est un théorème d arithmétique publié en 1926 par le mathématicien canadien Samuel Beatty qui donne une condition nécessaire et suffisante pour que deux suites pseudo arithmétiques partitionnent . Sommaire 1 Énoncé 2 Exemple … Wikipédia en Français
Beatty — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Beatty est un toponyme et un patronyme pouvant désigner : Sommaire 1 Toponyme 1.1 Canada … Wikipédia en Français
Samuel Beatty — Pour les articles homonymes, voir Beatty. Samuel Beatty (1881 1970) était un mathématicien canadien. On lui doit le théorème de Beatty … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… … Wikipédia en Français
Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de beatty