Théorème de Meyers
- Théorème de Meyers
-
Théorème de Bonnet-Schoenberg-Myers
Le théorème de Bonnet-Schoenberg-Myers est un théorème bien connu de la géométrie riemannienne. Il montre comment des contraintes locales sur une métrique riemannienne imposent des conditions globales sur la géométrie de la variété. Sa démonstration repose sur une utilisation classique de la formule de la seconde variation.
Théorème : Si une variété riemannienne complète a une courbure sectionnelle minorée par une constante strictement positive δ, alors son diamètre est borné par 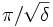 :
:
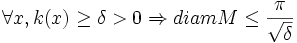
En particulier, M est compacte.
Le cas d'égalité a été étudié :
- Sous les notations précédentes, si le diamètre de M est égal à
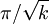 , alors (M,g) est isométrique à la sphère euclidienne de rayon
, alors (M,g) est isométrique à la sphère euclidienne de rayon 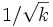 .
.
Le théorème de Meyer a le corollaire bien connu suivant :
- Le groupe fondamental d'une variété riemannienne compacte de courbure positive est un groupe fini.
 Portail des mathématiques
Portail des mathématiques
Catégories : Géométrie riemannienne | Théorème de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Meyers de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème de Meyers-Serrin H=W — En analyse fonctionnelle, le théorème de Meyers Serrin (de) concerne l équivalence de deux définitions des espaces de Sobolev. Sommaire 1 Définitions préalables 2 … Wikipédia en Français
Hall [3] — Hall (spr. haol), 1) Sir James, Baronet von Dunglaß, Geolog, geb. 17. Jan. 1761 in Dunglaß, gest. 23. Juni 1832 in Edinburg, lieferte experimentelle Beweise für die Ansichten Huttons, des ersten wichtigen Gegners von Werner, womit er zugleich die … Meyers Großes Konversations-Lexikon
Medizīn — (lat. Medicina, v. mederi. helfen, heilen; Heilkunde und Heilkunst), die Wissenschaft vom Menschen im gesunden und kranken Zustand und die Kunst, die Gesundheit zu erhalten, der Krankheit vorzubeugen und die Heilung zu fördern. Die heutige M.… … Meyers Großes Konversations-Lexikon
Espace de Sobolev — Les espaces de Sobolev sont des espaces fonctionnels. Plus précisément, un espace de Sobolev est un espace vectoriel de fonctions muni de la norme obtenue par la combinaison de la norme norme Lp de la fonction elle même ainsi que de ses dérivées… … Wikipédia en Français
Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Trace (algèbre) — Pour les articles homonymes, voir Trace. En algèbre linéaire, la trace d une matrice carrée A est définie comme la somme de ses coefficients diagonaux et notée Tr(A). La trace peut être vue comme une forme linéaire sur l espace vectoriel des… … Wikipédia en Français
Mécanique de la rupture — La mécanique de la rupture tend à définir une propriété du matériau qui peut se traduire par sa résistance à la rupture fragile (fracture). Car si les structures sont calculées pour que les contraintes nominales ne dépassent pas, en règle… … Wikipédia en Français
Liste geflügelter Worte/P — Geflügelte Worte A B C D E F G H I J K L M N O P Q R S T U V W Y Z Inhaltsverzeichnis … Deutsch Wikipedia
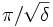 :
: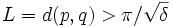 . Soit une géodésique
. Soit une géodésique ![\gamma:[0,L]\rightarrow M](/pictures/frwiki/54/62853359d37138ca6b3d5217e68a1190.png) d'origine γ(0) = p et d'extrémité γ(L) = q. Prenons v un vecteur dans TpM, orthogonal à γ'(0). Introduisons le champ de vecteurs parallèle Z le long de γ d'origine Z(0) = v. Posons :
d'origine γ(0) = p et d'extrémité γ(L) = q. Prenons v un vecteur dans TpM, orthogonal à γ'(0). Introduisons le champ de vecteurs parallèle Z le long de γ d'origine Z(0) = v. Posons :
![[0,L]\rightarrow M](/pictures/frwiki/102/f018b91debe0fd701bd20119c4379037.png) d'origine p et d'extrémité q avec c0 = γ et
d'origine p et d'extrémité q avec c0 = γ et 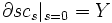 . La formule de la variation seconde, appliquée au champ de vecteurs Y, donne alors :
. La formule de la variation seconde, appliquée au champ de vecteurs Y, donne alors :
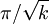 , alors (M,g) est isométrique à la sphère euclidienne de rayon
, alors (M,g) est isométrique à la sphère euclidienne de rayon 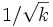 .
.
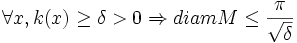
![Y(t)=\sin\left[\frac{\pi t}{L}\right].Z(t)](/pictures/frwiki/102/ff9a6ddb6aac0e56f572e4f2cd9017fa.png)
![Y'(t)=\frac{\pi}{L}\cos\left[\frac{\pi t}{L}\right] Z(t)](/pictures/frwiki/97/af11e446dccd9eab98f9977aba5090fb.png)
![\frac{\partial^2 long c_s}{\partial s^2}=\int_0^L \left[ \frac{\pi^2}{L^2}\cos^2\left[\frac{\pi t}{L}\right] - k(\gamma'(t),Y(t))\sin^2\left[\frac{\pi t}{L}\right]\right] dt\leq \frac{\pi^2 -\delta L^2}{2L}<0](/pictures/frwiki/48/048f1ae066b6f13dead10cd71770fdf9.png)