Théorème de Brahmagupta
- Théorème de Brahmagupta
-
En mathématiques, le théorème de Brahmagupta donne une condition nécessaire sur la perpendicularité des diagonales d'un quadrilatère inscriptible dans un cercle.
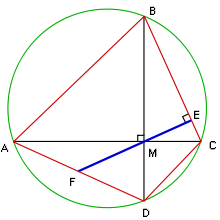
Théorème — Si un quadrilatère inscriptible a des diagonales perpendiculaires alors toute droite coupant perpendiculairement un côté quelconque du quadrilatère et passant par l'intersection des deux diagonales partage le côté opposé en deux parties égales.
Il est nommé ainsi en l'honneur du mathématicien Brahmagupta.
Démonstration
On suppose que ABCD est un quadrilatère inscriptible qui a ses diagonales perpendiculaires, et nous voulons prouver que AF = FD. Nous allons donc montrer que AF et FD sont tous les deux égales à FM.
Les angles FAM et CBM sont égaux (ce sont des angles inscrits qui interceptent le même arc de cercle). De plus, les angles CBM et CME sont des angles complémentaires à l'angle BCM. Et enfin, les angles CME et FMA sont égaux en tant qu'angles opposés par le sommet. Finalement, AFM est un triangle isocèle, et par conséquent ses côtés AF et FM sont égaux.
La démonstration que FD = FM est similaire. Les angles FDM, BCM, BME et DMF sont tous égaux, donc DFM est un triangle isocèle, d'où FD = FM. Il s'ensuit que AF = FD, ce qui démontre le théorème.
Voir aussi
Lien interne
Liens externes
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Brahmagupta de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Brahmagupta — (ब्रह्मगुप्त) (Multân, 598–668) est un mathématicien indien. Brahmagupta est l un des plus importants mathématiciens tant de l Inde que de son époque. On lui connaît deux ouvrages majeurs : le Brâhma Siddhânta (ब्रह्म सिद्धान्त) (628) et le… … Wikipédia en Français
Theoreme des deux carres de Fermat — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… … Wikipédia en Français
Théorème de Fermat sur les sommes de deux carrés — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… … Wikipédia en Français
Théorème des deux carrés — de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons… … Wikipédia en Français
Théorème des deux carrés de fermat — Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons différentes il peut … Wikipédia en Français
Théorème des deux carrés de Fermat — Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons différentes il peut … Wikipédia en Français
Identite de Brahmagupta — Identité de Brahmagupta En mathématiques, l identité de Brahmagupta est une formule utilisée pour la résolution d équations diophantiennes. Elle est ancienne, Diophante d Alexandrie un mathématicien grec vivant probablement au IIIe siècle… … Wikipédia en Français
Identité De Brahmagupta — En mathématiques, l identité de Brahmagupta est une formule utilisée pour la résolution d équations diophantiennes. Elle est ancienne, Diophante d Alexandrie un mathématicien grec vivant probablement au IIIe siècle établit un cas particulier … Wikipédia en Français
Identité de brahmagupta — En mathématiques, l identité de Brahmagupta est une formule utilisée pour la résolution d équations diophantiennes. Elle est ancienne, Diophante d Alexandrie un mathématicien grec vivant probablement au IIIe siècle établit un cas particulier … Wikipédia en Français
Formule de Brahmagupta — En géométrie euclidienne, la formule de Brahmagupta, trouvée par Brahmagupta, est une généralisation de la formule de Héron à l aire d un quadrilatère convexe inscriptible (c est à dire dont les sommets se situent sur un même cercle), uniquement… … Wikipédia en Français