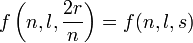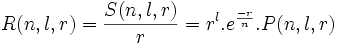Théorie de schrödinger de l'atome d'hydrogène

Théorie de Schrödinger de l'atome d'hydrogène

Pour consulter un article plus général, voir : atome.

Cet article est un complément pour l'article sur l'atome d'hydrogène et la Théorie de Pauli de l'atome d'hydrogène.

On considère que les harmoniques sphériques, l'équation 1D de Leibniz-Schrodinger ainsi que l'équation radiale-réduite sont des préacquis.

Pour cet article initial sur l'atome d'hydrogène, on va vérifier directement sur l'équation radiale-réduite en :

$f\left(n,l,\frac{2r}{n}\right)= f(n, l, s)$

et que les valeurs données par les tables mathématiques pour les couches K , L et M, sont exactes:

$R(n, l, r) = \frac{S(n, l, r)}{r} = r^l . e^{\frac{-r}{n}} . P(n, l, r)$

( Cet article à recours aux équations pour éviter une approche purement descriptive ! ).

Couche K

Pour la couche K, on l'a déjà vu l'orbitale 1s :

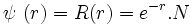$\psi\ (r) = R(r) = e^{-r} . N$ ,

avec N = 2 pour les couches K , L et M, sont exactes, vérifions-le :

R(r) est bien orthonormé sur l'intervalle r > 0 ;
l'équation radiale-réduite est automatiquement satisfaite puisque P = constante et k = 0.

Couche L

Pour la Couche L il y a 1 orbitale 2s , et 3 orbitales 2p :

Orbitales 2p (de Rydberg) :

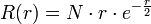$R(r) = N\cdot r\cdot e^{-\frac{r}{2}}$ .

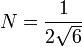La normalisation conduit à $N = \frac{1}{2\sqrt{6}}$ ,

mais il faudra encore multiplier par 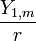$\frac{Y_{1,m}}{r}$ , avec $m = - 1,0,1$ .

Et avec 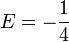$E=-\frac{1}{4}$ ( $n = 2$ , $l = 1$ donc $k = 0$ ), l'équation radiale-réduite est satisfaite, on l'a déjà vu.

Orbitale 2s : il y a 1 nœud, $k = 1$ :

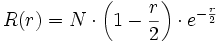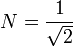$R(r)=N\cdot\left(1-\frac{r}{2}\right)\cdot e^{-\frac{r}{2}}$ avec $N = \frac{1}{\sqrt{2}}$ .

L'équation radiale-réduite est

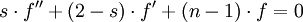$s\cdot f'' + (2-s)\cdot f' + (n-1)\cdot f = 0$ ,

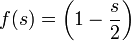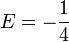avec $f(s)= \left(1-\frac{s}{2}\right)$ : soit $(2 - s)( - 1 / 2) + (n - 1)(1 - s / 2) = 0$ , ou encore $E=-\frac{1}{4}$ .

Couche M

Couche M : 1 orbitale 3s , 3 orbitales 3p et 5 orbitales 3d :

Orbitales 3d (de Rydberg) donc

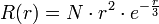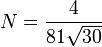$R(r) = N\cdot r^2\cdot e^{-\frac{r}{3}}$ avec $N = \frac{4}{81\sqrt{30}}$ .

Il faudra multiplier par 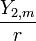$\frac{Y_{2,m}}{r}$ avec $m = - 2, - 1,0,1,2$ .

L'énergie est 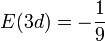$E(3d) = -\frac{1}{9}$ (déjà vu f(s) = cste).

Orbitales 3p , avec 1 nœud :

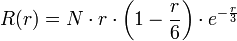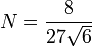$R(r) = N\cdot r\cdot\left(1-\frac{r}{6}\right)\cdot e^{-\frac{r}{3}}$ avec $N = \frac{8}{27\sqrt{6}}$ .

Il faudra multiplier par 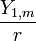$\frac{Y_{1,m}}{r}$ avec $m = - 1,0,1$ .

Montrer que 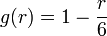$g(r)=1-\frac{r}{6}$ vérifie $r g'' + (6 - r) g' + g = 0$ est assez facile.

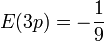Finalement, l'énergie vaut bien $E(3p)=-\frac{1}{9}$ .

Orbitale sphérique 3s, avec 2 nœuds :

$R(r) = N\cdot (r-a)(r-b)\cdot e^{-\frac{r}{3}}$ ,

et cette fois, il faut vérifier que

$f (3,0, s) = (s - a')(s - b') = s 2 - S s + P$

satisfait à

$s f'' + (2 - s) f' + 2 f = 0$ ,

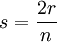ce qui est assez aisé : f est le Polynôme $s 2 - 6 s + 6$ , soit avec $s=\frac{2r}{n}$ ,

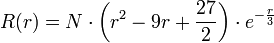$R(r)=N\cdot\left(r^2-9r+\frac{27}{2}\right)\cdot e^{-\frac{r}{3}}$ : la probabilité de trouver l'électron voisin de $r = a$ ou $r = b$ , soit 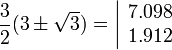$\frac{3}{2}(3\pm\sqrt{3}) = \left|\begin{array}{l}7.098\\1.912\end{array}\right.$ est nulle.

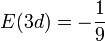Finalement, l'énergie vaut $E(3d)= -\frac{1}{9}$ .

Conclusion

L'énergie la plus basse (n=1, E = E1) correspond à 1seule orbitale 1s. Puis la couche L( n=2 E = E2 = E1/2²)correspond à 1+3 orbitales, une 2s et trois 2p. La couche M ( n=3, E = E3 = E1/3²) correspond à 1+3+5 orbitales, une 3s (avec deux nœuds en 1.9 et 7.1), trois 3p (avec un nœud en r=6) et enfin cinq 3d (sans nœud).

Liens externes

Christian Magnan, Texte sur la théorie de Schrödinger

Portail de la physique

Ce document provient de « Th%C3%A9orie de Schr%C3%B6dinger de l%27atome d%27hydrog%C3%A8ne ».

Catégories : Article à recycler (physique) | Atome | Théorie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorie de schrödinger de l'atome d'hydrogène de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Theorie de Schrodinger de l'atome d'hydrogene — Théorie de Schrödinger de l atome d hydrogène Pour consulter un article plus général, voir : atome. Cet article est un complément pour l article sur l atome d hydrogène et la Théorie de Pauli de l atome d hydrogène. On considère que les… … Wikipédia en Français
Théorie de Schrodinger de l'atome d'hydrogène — Théorie de Schrödinger de l atome d hydrogène Pour consulter un article plus général, voir : atome. Cet article est un complément pour l article sur l atome d hydrogène et la Théorie de Pauli de l atome d hydrogène. On considère que les… … Wikipédia en Français
Théorie de Schrödinger de l'atome d'hydrogène — Pour consulter un article plus général, voir : atome. Cet article est un complément pour l article sur l atome d hydrogène et la Théorie de Pauli de l atome d hydrogène. On considère que les harmoniques sphériques, l équation 1D de Leibniz… … Wikipédia en Français
Theorie de Pauli de l'atome d'hydrogene — Théorie de Pauli de l atome d hydrogène Pour consulter un article plus général, voir : atome. Cet article suit l article atome d hydrogène. La résolution de l équation de Schrödinger, écrite en coordonnées polaires, se découple des variables … Wikipédia en Français
Théorie de pauli de l'atome d'hydrogène — Pour consulter un article plus général, voir : atome. Cet article suit l article atome d hydrogène. La résolution de l équation de Schrödinger, écrite en coordonnées polaires, se découple des variables (θ,φ) et conduit à une équation à une… … Wikipédia en Français
Théorie de Pauli de l'atome d'hydrogène — Pour consulter un article plus général, voir : atome. Cet article suit l article atome d hydrogène. La résolution de l équation de Schrödinger, écrite en coordonnées polaires, se découple des variables (θ,ϕ) et conduit à une équation à une… … Wikipédia en Français
Atome D'hydrogène — Pour consulter un article plus général, voir : atome. L atome d hydrogène est un atome composé d un proton et d un électron. C est l atome le plus simple qui existe et le premier élément de la classification périodique. L électron et le… … Wikipédia en Français
Atome d'hydrogene — Atome d hydrogène Pour consulter un article plus général, voir : atome. L atome d hydrogène est un atome composé d un proton et d un électron. C est l atome le plus simple qui existe et le premier élément de la classification périodique. L… … Wikipédia en Français
Atome d'hydrogène — Pour consulter un article plus général, voir : atome. L atome d hydrogène est un atome composé d un proton et d un électron. C est l atome le plus simple et le premier élément de la classification périodique. Son électron et son proton sont… … Wikipédia en Français
Orbitale de l'atome d'hydrogene — Orbitale de l atome d hydrogène On appelle orbitales de l atome d hydrogène, les solutions stationnaires de l équation de Schrodinger de l atome d hydrogène. (voir Théorie de Schrödinger de l atome d hydrogène). À chaque état stationnaire… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorie de schrödinger de l'atome d'hydrogène