Série de Lyman
- Série de Lyman
-
La série de Lyman correspond à toutes les transitions électroniques des états excités (n ≥ 2) de l'atome d'hydrogène vers son état fondamental (n = 1) et se traduit par l'émission d'une série de longueurs d'ondes en physique.
Le nombre n est le nombre quantique principal désignant le niveau d’énergie de l’électron. Les états de transitions sont nommés par des lettres grecques :
| Transition |
Notation de Lyman |
Notation de Siegbahn |
Notation IUPAC |
de n = 2 vers n = 1
(couche L vers couche K) |
α-Lyman |
Kα |
K-L? |
de n = 3 vers n = 1
(couche M vers couche K) |
β-Lyman |
Kβ1 |
K-M3 |
de n = 4 vers n = 1
(couche N vers couche K) |
γ-Lyman |
Kβ2 |
K-N? |
| … |
La première raie du spectre ultraviolet (UV) de la série de Lyman fut découverte en 1906 par un physicien de Harvard Theodore Lyman qui étudiait le spectre UV en électrisant des molécules d’hydrogène. Le reste des raies du spectre fut découvert par ce même chercheur entre 1906 et 1914.
Le spectre de radiation émis par l’hydrogène est non continu. On retrouve ici une illustration de la première série de raies émises par l’hydrogène :
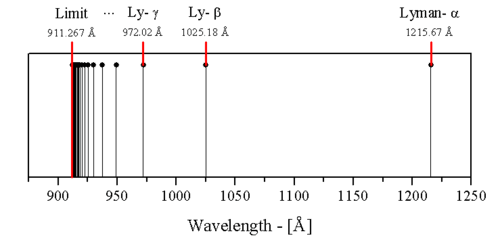
Historiquement, l’explication de la nature d’un tel spectre posa de sérieux problèmes en physique, personne ne pouvait prédire la longueur d’onde du spectre de l'hydrogène jusqu'à ce que Johannes Rydberg propose une formule empirique qui résout le problème en 1888. Il testa plusieurs formules afin d'en trouver une correspondant aux raies connues. Il put alors prédire les raies non encore découvertes avec cette même formule :
où n est un entier naturel supérieur ou égal à 2.
Ainsi donc, les raies observées correspondent à des longueur d'onde telles que n = 2 jusqu'à n = 
(de droite à gauche sur le spectre ci-dessus).
Les longueurs d’ondes en nanomètres (nm) dans la série de Lyman sont :
| Transition |
|
longueur d'onde (nm) |
| 2-1 |
: |
121,5 |
| 3-1 |
: |
102,5 |
| 4-1 |
: |
97,2 |
| 5-1 |
: |
94,9 |
| 6-1 |
: |
93,7 |
| 7-1 |
: |
93,0 |
| 8-1 |
: |
92,6 |
| 9-1 |
: |
92,3 |
| 10-1 |
: |
92,1 |
| 11-1 |
: |
91,9 |
| Limite : 91,15 nm |
Voir aussi
Source
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Série de Lyman de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Serie de Lyman — Série de Lyman La série de Lyman correspond à toutes les transitions électroniques des états excités (n ≥ 2) de l atome d hydrogène vers son état fondamental (n = 1) et se traduit par l émission d une série de longueurs d ondes en physique. Le… … Wikipédia en Français
Série de lyman — La série de Lyman correspond à toutes les transitions électroniques des états excités (n ≥ 2) de l atome d hydrogène vers son état fondamental (n = 1) et se traduit par l émission d une série de longueurs d ondes en physique. Le nombre n est le… … Wikipédia en Français
Serie de Lyman — En Química, la Serie de Lyman es el conjunto de lineas que resultan de la emisión del átomo del hidrógeno cuando un electrón transita de n ≥ 2 a n = 1 (donde n representa el número cuántico principal referente al nivel de energía del electrón).… … Wikipedia Español
série de Lyman — Laimano serija statusas T sritis fizika atitikmenys: angl. Lyman series vok. Lyman Serie, f rus. серия Лаймана, f pranc. série de Lyman, f … Fizikos terminų žodynas
Serie de Balmer — Série de Balmer La série de Balmer est un terme de physique atomique qui désigne une série de raies spectrales de l atome d hydrogène correspondant à une transition électronique d un état quantique de nombre principal n > 2 vers l état de… … Wikipédia en Français
Serie de Paschen — Série de Paschen En physique, la série de Paschen (appelée également série de Ritz Paschen) désigne la série de transitions et les raies spectrales correspondantes de l atome d hydrogène lorsqu un électron passe de n ≥ 4 à n = 3, où n est le… … Wikipédia en Français
Série de balmer — La série de Balmer est un terme de physique atomique qui désigne une série de raies spectrales de l atome d hydrogène correspondant à une transition électronique d un état quantique de nombre principal n > 2 vers l état de niveau 2. L… … Wikipédia en Français
Série de paschen — En physique, la série de Paschen (appelée également série de Ritz Paschen) désigne la série de transitions et les raies spectrales correspondantes de l atome d hydrogène lorsqu un électron passe de n ≥ 4 à n = 3, où n est le nombre quantique… … Wikipédia en Français
Serie de Brackett — Série de Brackett En physique, la série de Brackett désigne la série de transitions et les raies spectrales correspondantes de l atome d hydrogène lorsqu un électron passe de n ≥ 5 à n = 4, où n est le nombre quantique principal de l électron. La … Wikipédia en Français
Serie de Humphreys — Série de Humphreys La série de Humphreys est un terme de physique atomique qui désigne une série de raies spectrales de l atome d hydrogène correspondant à une transition électronique d un état quantique de nombre principal n > 6 vers l état… … Wikipédia en Français
