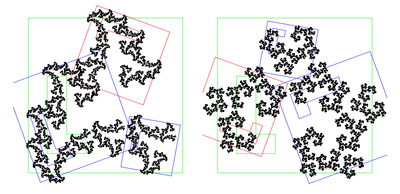
Système de fonctions itérées

Fractales construites à partir d'un système de 3 similitudes

Fractale "Flame" construite à partir d'un système itéré de fonctions non linéaires, avec le programme Apophysis

La théorie des systèmes de fonctions itérées ou IFS (d'après le nom anglais Iterated Function System) est une théorie mathématique développée par John Hutchinson en 1981, utilisée dans le cadre de la géométrie fractale (depuis les travaux de Barnsley en 1988 et son livre Fractals Everywhere). Cette théorie est entièrement fondée sur les invariances par changement d'échelle.

Barnsley a démontré, avec le Théorème du collage, que tout ensemble de points peut être approximé par un IFS.

Un IFS peut être la représentation fonctionnelle d'une fractale. Cela donne une théorie parfaitement définie mathématiquement qui permet de nombreuses études sur les fractales (Continuité, dérivabilité, approximation...)

Un IFS est un ensemble de N fonctions contractantes dans un espace métrique M.

On définit à partir des T_i une nouvelle fonction T, elle aussi contractante sur l'ensemble des parties de M muni de la distance de Hausdorff, par l'expression .

Le théorème du point fixe assure l'existence et l'unicité d'un sous-ensemble fixe tel que T(F) = F. F est appelé attracteur de l'IFS. F est alors une fractale.

En pratique, F est obtenue comme la limite Tⁿ(F₀) pour où F₀ est un compact quelconque. C'est de cette propriété qui vient le mot itéré car on se restreint souvent à l'étude de T^N(F₀) une approximation de la fractale.

Remarques :

• Les IFS ne servent pas uniquement à la modélisation des fractales, même si c'est dans ce cadre-là qu'elles sont le plus utilisées.
• La plupart des fonctions des IFS sont des fonctions affines. On appelle flame IFS des fractales obtenues par des fonctions non linéaires.

Dimension fractale

Si la condition d'ensemble ouvert est respectée, la valeur de la dimension de Hausdorff D de l'attracteur d'un IFS composé de k similitudes contractantes de rapport c_i, satisfait à l'équation suivante:

Dans le cas de fonctions affines ou non linéaires, cette équation n'est plus valable.

Exemples

La fougère de Barnsley, élaborée par un système de 3 fonctions affines

• L'ensemble de Cantor

Fonction 1 : homothétie de rapport 1/3 par rapport au point (0,0,0)

Fonction 2 : homothétie de rapport 1/3 par rapport au point (1,0,0)

• Le tapis de Sierpinski de sommets P₁, P₂, P₃ et P₄ : 4 homothéties de rapport 1/2 par rapport à chacun des points P_i

• La fougère de Barnsley, construite à partir de trois contractions affines (rouge, bleu et cyan sur l'illustration)

Voir aussi

• Fractale
• Jeu du chaos, une version simplifiée proposée par Barnsley.
• Théorème du collage

Références et logiciels

• (en) Kenneth Falconer, Fractal geometry: Mathematical foundations and applications, John Wiley and Sons, 1990 (ISBN 0-471-92287-0), p. 113–117,136 
• John E. Hutchinson, « Fractals and self similarity », dans Indiana Univ. Math. J., vol. 30, 1981, p. 713–747 [lien DOI] 
• Apophysis, générateur de fractales supportant des fonctions non linéaires.
• Glito, programme libre permettant d'explorer les IFS de dimension 2 (applications affines, fonction sinusoïdales, ensemble de Julia) - :

• Portail des mathématiques