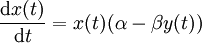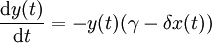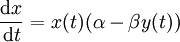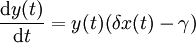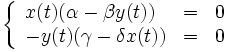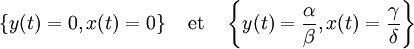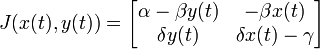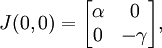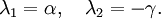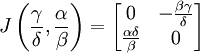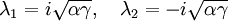- Système de Lotka-Volterra
-
Équations de Lotka-Volterra
En mathématiques, les équations de Lotka-Volterra, que l'on désigne aussi sous le terme de "modèle proie-prédateur", sont un couple d'équations différentielles non-linéaires du premier ordre, et sont couramment utilisées pour décrire la dynamique de systèmes biologiques dans lesquels un prédateur et sa proie interagissent. Elles ont été proposées indépendamment par Alfred James Lotka en 1925 et Vito Volterra en 1926.
Ce système d'équations est classiquement utilisé comme modèle pour la dynamique du lynx et du lièvre des neiges, pour laquelle de nombreuses données de terrain ont été collectées sur les populations des deux espèces par la Compagnie de la baie d'Hudson au XIXe siècle. Il a aussi été employé par John Allan Hobson pour décrire les relations entre les neurones cholinergiques responsables du sommeil paradoxal et les neurones aminergiques liées à l'état de veille.[réf. nécessaire]
Sommaire
Les équations
Elles s'écrivent fréquemment :
où
- x(t) est l'effectif des proies;
- y(t) est l'effectif des prédateurs;
- t est le temps;
- dx(t) / dt et dy(t) / dt représentent les taux de croissance des populations au cours du temps;
- α, β, γ et δ sont des paramètres caractérisant les interactions entre les deux espèces.
Signification physique des équations
Une fois développées, les équations prennent une forme utile pour une interprétation physique.
Proies
L'équation de la proie devient :
Les proies sont supposées avoir une source illimitée de nourriture et se reproduire exponentiellement si elles ne sont soumises à aucune prédation ; cette croissance exponentielle est représentée dans l'équation ci-dessus par le terme αx(t). Le taux de prédation sur les proies est supposé proportionnel à la fréquence de rencontre entre les prédateurs et les proies ; il est représenté ci-dessus par βx(t)y(t). Si l'un des termes x(t) ou y(t) est nul, alors il ne peut y avoir aucune prédation.
Avec ces deux termes, l'équation peut alors être interprétée comme : la variation du nombre de proies est donnée par sa propre croissance moins le taux de prédation qui leur est appliqué.
Prédateurs
L'équation du prédateur devient :
Dans cette équation, δx(t)y(t) représente la croissance de la population prédatrice. (Notons la similarité avec le taux de prédation ; cependant, une constante différente est utilisée car la vitesse à laquelle la population des prédateurs augmente n'est pas nécessairement égale à celle à laquelle il consomme la proie). De plus, γy(t) représente la mort naturelle des prédateurs ; c'est une décroissance exponentielle. L'équation représente donc la variation de la population de prédateurs en tant que croissance de cette population, diminuée du nombre de morts naturelles.
Solutions de l'équation

Les équations admettent des solutions périodiques qui n'ont pas d'expressions simple à l'aide des fonctions trigonométriques habituelles. Néanmoins, une solution approximative linéarisée offre un mouvement harmonique simple, avec la population des prédateurs en retard de 90° (un quart de période) sur celle des proies.
Dynamique du système
Dans le modèle utilisé, les prédateurs prospèrent lorsque les proies sont nombreuses, mais finissent par épuiser leurs ressources et déclinent. Lorsque la population de prédateur a suffisamment diminué, les proies profitant du répit se reproduisent et leur population augmente de nouveau. Cette dynamique se poursuit en un cycle de croissance et déclin.
Equilibres de la population
Un état d'équilibre de la population est observé quand aucune des deux populations en présence n'évolue, c'est-à-dire quand les dérivées correspondantes sont nulles, ce qui se traduit par le système d'équations :
qui a pour solutions :
La première solution correspond à une extinction définitive des deux espèces, la seconde à des valeurs pour les deux populations, dépendant des quatre paramètres α, β, γ et δ, qui restent stables indéfiniment.
Stabilité des points fixes
La stabilité des points fixes peut être déterminée par une linéarisation du système aux dérivées partielles. La matrice jacobienne du système est
Au premier point fixe (0,0), cette matrice prend la valeur :
qui a pour valeurs propres :
Ces valeurs propres sont toujours de signes opposés, ce qui montre que ce point fixe est un point selle. Ce n'est donc pas un point fixe stable, ce qui montre en particulier que, suivant ce modèle, l'extinction des deux espèces en jeu est difficile à obtenir.
Second point fixe
En évaluant la matrice jacobienne en le second point fixe, la valeur suivante est obtenue :
et elle a pour valeurs propres :
Ce point fixe est donc un foyer et plus particulièrement un centre, ce qui signifie que les populations de proies et prédateurs oscillent autour de leurs valeurs en ce point fixe.
Voir également
Bibliographie
- E. R. Leigh (1968) The ecological role of Volterra's equations, in Some Mathematical Problems in Biology - a modern discussion using Hudson's Bay Company data on lynx and hares in Canada from 1847 to 1903.
- Understanding Nonlinear Dynamics. Daniel Kaplan et Leon Glass.
- V. Volterra. Variations and fluctuations of the number of individuals in animal species living together. In Animal Ecology. McGraw-Hill, 1931. Traduit de l'édition de 1928 par R. N. Chapman.
Liens externes
- Lotka-Volterra Predator-Prey Model by Elmer G. Wiens
- Modèle de Lotka-Volterra
- Portail de l’écologie
- Portail des mathématiques
Catégories : Écologie des communautés | Équation différentielle
Wikimedia Foundation. 2010.