- Système de Hilbert
-
Système à la Hilbert
En logique, les systèmes à la Hilbert servent à définir les déductions formelles en suivant un modèle proposé par David Hilbert au début du XXe siècle : un grand nombre d'axiomes logiques exprimant les principales propriétés de la logique que l'on combine au moyen de quelques règles, notamment la règle de modus ponens, pour dériver de nouveaux théorème. Les systèmes à la Hilbert héritent du système défini par Gottlob Frege et constituent les premiers systèmes déductifs, avant l'apparition de la déduction naturelle ou du calcul des séquents.
Sommaire
Définition
Calcul propositionnel
On considère l'ensemble des formules du calcul propositionnel. Rappelons qu'il s'agit des formules finies que l'on peut construire inductivement à partir des variables propositionnelles au moyen des connecteurs logiques.
On se donne un ensemble d'axiomes logiques qui sont des formules valides du calcul propositionnel. Une déduction est une suite de formules telle que chaque formule A apparaissant dans cette suite vérifie l'une des conditions suivantes :
- A est une instance d'axiome (ou de théorème), c’est-à-dire l'un des axiomes logiques (ou l'un des théorèmes déjà démontrés) dans lequel les variables propositionnelles sont remplacées par des formules ;
- il existe deux formules précédant
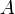 qui sont de la forme
qui sont de la forme 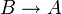 et
et 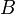 ; on dit alors que
; on dit alors que 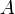 est obtenue par modus ponens entre ces deux formules.
est obtenue par modus ponens entre ces deux formules.
On représente une déduction en écrivant les formules ligne par ligne et en adjoignant un commentaire à chaque ligne pour expliquer comment la formule correspondant a été obtenue.
Il existe plusieurs choix possibles de systèmes axiomatiques du calcul propositionnel. On en donne un ici relativement verbeux mais assez intuitif.
- Axiomes pour l'implication. Le choix de ces deux axiomes un peu étranges se justifie par le fait qu'ils simplifient la démonstration du théorème de déduction :
- Axiome K :
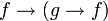 ;
; - Axiome S :
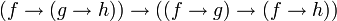 .
.
- Axiome K :
- Axiomes pour la négation. On donne deux des principales variantes de ces axiomes ; à titre d'exemple le lecteur pourra choisir l'une d'elles et essayer de trouver une déduction de l'autre :
- Raisonnement par l'absurde :
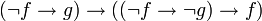 ;
; - Contraposition :
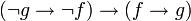 .
.
- Raisonnement par l'absurde :
- Axiomes pour la conjonction :
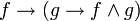 ;
;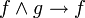 ,
, 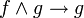 .
.
- Axiomes pour la disjonction :
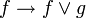 ,
, 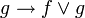 ;
;- Raisonnement par cas :
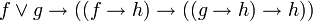 .
.
Exemple de déduction
Voici une déduction de l'identité
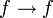 :
: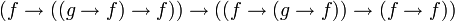 (instance de l'axiome S)
(instance de l'axiome S) (instance de l'axiome K)
(instance de l'axiome K)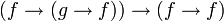 (modus ponens entre 1 et 2)
(modus ponens entre 1 et 2)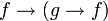 (instance de l'axiome K)
(instance de l'axiome K)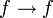 (modus ponens entre 3 et 4)
(modus ponens entre 3 et 4)
Le théorème de déduction
Comme on voit sur l'exemple précédent, il est assez malcommode de démontrer les propriétés les plus simples. C'est pourquoi on étend le système en ajoutant la possibilité d'utiliser des hypothèses, c’est-à-dire des formules non prouvées. Ainsi au lieu de démontrer
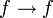 , on se contenterait de démontrer
, on se contenterait de démontrer  en utilisant l'hypothèse
en utilisant l'hypothèse  , ce qui revient à écrire une démonstration d'une seule ligne.
, ce qui revient à écrire une démonstration d'une seule ligne.Un autre exemple de démonstration avec hypothèse est donné par la transitivité de l'implication : en se donnant les hypothèses
 ,
,  et
et  , on démontre que
, on démontre que 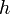 :
: (hypothèse)
(hypothèse) (hypothèse)
(hypothèse)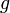 (modus ponens entre 2 et 1)
(modus ponens entre 2 et 1) (hypothèse)
(hypothèse)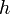 (modus ponens entre 4 et 3)
(modus ponens entre 4 et 3)
La question se pose alors de savoir si à partir d'une preuve avec hypothèses on peut récupérer une preuve sans ; par exemple peut-on à partir de la preuve ci-dessus déduire l'existence d'une preuve de
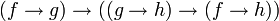 ? La réponse est oui, et c'est ce qu'énonce le théorème de déduction : si on a une démonstration d'une formule A utilisant une hypothèse B alors on peut construire une démonstration de
? La réponse est oui, et c'est ce qu'énonce le théorème de déduction : si on a une démonstration d'une formule A utilisant une hypothèse B alors on peut construire une démonstration de 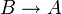 qui n'utilise plus cette hypothèse, soit si B|- A, alors |-
qui n'utilise plus cette hypothèse, soit si B|- A, alors |- 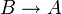 .
.L'utilisation du théorème de déduction permet de simplifier considérablement la recherche de preuves dans les systèmes à la Hilbert. C'est un passage obligé d'une démonstration du théorème de complétude pour un tel système. Dans la déduction naturelle ou le calcul des séquents de Gerhard Gentzen le théorème de la déduction est en quelque sorte intégré comme règle primitive sous la forme d'introduction droite de l'implication.
- Portail des mathématiques
- Portail de la logique
Catégories : Logique mathématique | Logique | Méthode de démonstration
Wikimedia Foundation. 2010.
