Systeme d'unites stellaires

Cet article est un exemple d'utilisation des SUN ( Système d'unités naturelles ou Dahus ) pour l'étude d'une étoile ordinaire de la séquence principale du diagramme H-R ( Hertzsprung-Russell).

Il est issu de l'analyse de Weiskopff (CERN-1949, faire la physique simple).

• Une étoile sera considérée comme une boule homogène de rayon R , contenant N protons et N électrons, autogravitante, qui ne s'effondre pas car en son cœur se produit la fusion thermonucléaire de 4 protons en Helium(++): la température y est donc très élevée (de l'ordre de 10 millions de kelvins). Les photons qui sortent de cet immense four sont thermalisés et leur flux énergétique représente la luminosité L (en watts) de l'étoile.

Ce modèle excessivement simpliste donnera néanmoins , à peu de frais, en utilisant les Dahus, les éléments essentiels de compréhension du fonctionnement d'une étoile ordinaire.

Sommaire 1 Relation du Viriel 2 Limite supérieure de N 3 Conséquence : Nombre de Photons 4 Luminosité de l'étoile 5 Température et Puissance thermonucléaire 5.1 équilibre et stabilité 6 Température de surface 7 Durée de vie 8 Chimie stellaire 9 Naine blanche 10 Autres objets 11 Conclusion 12 Voir aussi

Relation du Viriel

Pour tout système en équilibre mécanique (via la loi de Newton) et thermique ( théorème de l'équipartition), l'énergie cinétique est l'opposée de l'énergie totale, elle-même égale à la moitié de l'énergie potentielle.

On peut donc écrire la relation du viriel :

3/2 N.kT ( protons) +3/2 N.kT (électrons) = 1/2 (3/5 GM². N²/R)

avec M := masse du proton. Le premièr terme est extensif ( ~ N), le deuxième non (~N²). En divisant par N et en ne gardant que les OdG ( Ordre de Grandeur), on obtient :

kT . R = GM². N

Limite supérieure de N

En fait il faut aussi tenir compte de l'énergie des photons qui peut être très grande : la théorie-Dahu du corps noir donne cette énergie par unité de volume :

E/V = d.u.[kT, 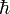c ]

le coefficient est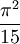

Cette énergie va déstabiliser l'étoile (on peut dire aussi que la pression de radiation va faire exploser l'étoile) si N est trop grand : il intervient alors dans ce calcul , un nombre caractéristique sans dimension qui est appelé nombre d'Avogadro stellaire :

Ce nombre vaut 2.2 10^57 et on pourra le comparer au rapport de la masse du soleil ( 2 10^30 kg) à celle d'un proton (5/3 10^(-27)kg ). Il va jauger la masse de l'étoile, qui est un paramètre capital, mais dont on verra que 0.1 N* < N < 100 N* : ainsi, il apparaît la règle de Wheeler ( cf article Système d'unités naturelles : en prenant le bon OdG, les résultats sont voisins de 1.

Conséquence : Nombre de Photons

Pour une étoile pas trop massive (ni trop dense comme il sera vu plus tard), on continuera à utiliser la relation du viriel kT.R = cste : cette relation exprime l'isentropie lumineuse , soit la conservation du nombre de photons : si l'étoile tend à perdre de sa température, elle gonfle , et le nombre de photons reste constant :

Luminosité de l'étoile

Il ne s'agit que d'un calcul grossier. Il consiste à dire que les photons ne sortent de l'étoile qu'après une marche au hasard, en se cognant sur les électrons, via la section efficace de Thomson :cette section vaut S= 8Pi/3 .ro² avec e²/ro = mc² ( et 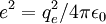);le libre parcours moyen d'un photon est donc l = a.a²/S , avec a = distance moyenne des électrons (en gros (Volume/N)^(1/3) ). Le temps de sortie d'un photon est donc (selon la loi de la diffusion d'Einstein):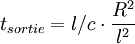

soit N.(ro²/R)/c : soit le résultat pseudo-paradoxal que le temps de sortie est d'autant plus grand que l'étoile est petite! ( mais alors la concentration de centres diffuseurs est plus grande, ce qui résout ce pseudo-paradoxe).

On trouve alors un résultat extraordinaire :chaque photon emmène en moyenne une luminosité kT/t(sortie) = c. (kT.R)/Nro² soit c.GM²/ro² QUI EST UNE CONSTANTE FONDAMENTALE , ne dépendant pas de la masse de l'étoile : L = d.u.[GM²,c,ro]!

En multipliant par le nb de photons, on trouve la luminosité totale de l'étoile :

Application numérique: prenons ro = 1 fm, L ~ 50/9 10^(-28)W et

L(totale)= 10^30 W.(N/N*)^3

On retrouve l'OdG de la luminosité de l'étoile et surtout la dépendance-loi-puissance en (N/N*)^3 . Evidemment tout ceci dépend de ro² , c’est-à-dire de la section de Thomson. Si l'on doit plutôt faire intervenir la section de Kramers qui dépend de la température , il faut modifier la théorie en conséquence.

Température et Puissance thermonucléaire

Le Dahu d'un réacteur nucléaire est assez difficile à calculer ; il exige de connaître l'effet tunnel quantique. En effet la réaction de fission ne peut se produire que si deux protons sont en contact, ie à une distance de femtomètre. La barrière d'énergie électrostatique à franchir est alors typiquement de Mc² = ~ 1 GeV . Cette température est très loin d'être atteinte dans le Soleil.

Effet tunnel : C'est parce que, comme Gamow l'a bien décrit, il suffit qu'une petite probabilité existe de passer cette barrière. La formule de Gamow-Wick-Corinne donne cette probabilité:

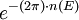
Ici n(E) est la fonction réciproque de E(n) donnant "les niveaux d'énergie de la barrière de Corinne renversée en puits" ( cf effet tunnel) : or cela est bien connu pour un puits coulombien :

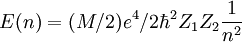[donc n= sqrt(E(1)/E)]

est la formule des niveaux de l'hydrogène adaptée à ce problème proton-antiproton. Plus E est grand et plus la probabilité est grande, mais aussi d'après la loi de Boltzmann, moins il y a de couples ayant cette énergie cinétique relative.

En définitive, l'optimum se trouve extrèmement bien "piqué" en énergie : c'est le "pic de Gamow" , donné par le maximum de -2Pi sqrt(E(1)/E) -E/kT ( donc Pi.sqrt(E(1)/E) = E/kT, par le théorème de Didon) et la probabilité par exp- 3(Pi².E(1)/kT)^(1/3).

Il suffit alors de multiplier cette probabilité (qui joue le rôle de facteur d'Arrhénius moyenné) par la vitesse de réaction nucléaire proportionnelle à la densité de protons au carré * le deltaH de la réaction. On obtient ainsi la puissance P(T) du réacteur thermo-nucléaire de fusion.

équilibre et stabilité

• Evidemment , il y a équilibre quand P(T) = Luminosité (T).

Mais il a été vu que cette luminosité était indépendante de T ( sous l'hypothèse de section efficace de Thomson). Donc la température est fixée par L, c’est-à-dire par la masse de l'étoile. Typiquement la température est de 1 keV. Un calcul aisé montre que, au voisinage de cette température, P(T) croît comme T^n avec n ~ 6,soit P(T) = L .(T/Te)^6 c-à-d que l'intersection P(T) = L a une température qui reste toujours voisine de 1keV;

• La stabilité de l'étoile est remarquable : si pour une raison quelconque le réacteur venait à s'emballer , il y aurait excès de puissance produite , et la TEMPERATURE DIMINUERAIT (en même temps que le rayon gonflerait (th du viriel)) et donc P(T) se calmerait : l'équilibre est stable par cet effet de "capacité calorifique négative".

Le rayon obtenu est pour N = N* environ R*= 1 Mkm , et R = R* (N/N*)

Température de surface

Oh Be A Fine Girl Kiss Me est la phrase classique qui permet de classer les étoiles depuis les chaudes vers les froides.

Dans le type de modèle qui vient d'être décrit, L ne dépend pas de T et T reste toujours voisin de 10 millions de kelvins. Donc la température de surface reste telle que :

4Pi.R².sigma.Ts^4 = L* (N/N*)^3 et comme R = R*.(N/N*) , Ts = Ts* (N/N^(1/4) .

Donc L/L* = (Ts/Ts*)^12 : c'est la loi d'échelle de H-R.

Typiquement, on sait que pour le soleil , L = 4 10^26W avec Ts = 5680K et R= 700 000 km. MAIS, le soleil n'est pas une boule homogène !!!Et les facteurs de forme sont importants. Il faut remplacer N par un Nefficace = k(forme).N , où k(forme) est pris en compte pour ajuster cette théorie simpliste à la réalité : on peut écrire les équations de EMDEN et réappliquer la théorie des Dahus à ces équations : on obtiendrait alors la valeur du facteur de forme.

Durée de vie

Quand tout l'hydrogène se sera transformé en hélium, l'énergie fournie sera 7 MeV .N = Eo.N

Le temps de vie de l'étoile est donc:

T_vie = (E0/(L*/N*)). (N*/N)^2

Une étoile 10 fois plus massique que le Soleil passera 100 fois moins de temps que le Soleil sur la séquence principale , c'est-à-dire environ 100 My. Dans l'intervalle 0.1 à 100 N*, les échelles de temps vont varier de 1 My à 1000 Gy ! On voit donc que l'Univers est peuplé d'étoiles fossiles et d'étoiles de 2^e ou enième génération.

Chimie stellaire

Ce chapitre est beaucoup plus difficile à traiter par les Dahus car chaque élément a ses propriétés de chimie nucléaire ( vitesse de réaction et deltaH). On ne peut que donner des idées d'OdG : l'Helium fusionnera en Carbone , puis le carbone en Azote et Oxygène , etc . jusqu'au Fer.

Les températures sont plus élevées, donc ont lieu à l'intérieur de l'étoile qui possèdera alors une structure en oignon avec une distribution d'éléments lourds vers le centre.

Puis si l'étoile perd son énergie , on a vu que sa température allait diminuer et qu'elle gonflerait : c'est le stade géante rouge comme l'étoile Betelgeuse ( fin de vie). Au-delà l'étoile souffle son enveloppe géante et le cœur s'effondre: c'est une nova , stade qui dure fort peu ( quelques mois). Le cœur devient une naine blanche.

Naine blanche

Dans une naine blanche, l'étoile ne s'effondre pas car le gaz d'électrons devient quantique (non relativiste). Au lieu 3/2 kT par électron , il faut comme en théorie du solide prendre la formule donnant l'énergie des électrons distants de a : on sait que cette énergie est de l'ordre de d.u[] = .

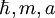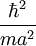En réécrivant le théorème du viriel, on aura cette fois

3/2kT + 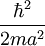- GM² N/a = 0 en OdG

La kT-température ne saurait être supérieure à GM²N/2a avec a = d.u. [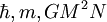] =  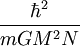: le volume V ~ Na³ varie comme 1/N² et la masse volumique en N^3 ! plus la naine est massique , plus elle est petite.

Autres objets

• pulsar == étoile à neutrons:

si la pression des électrons ne suffit pas , l'étoile s'effondre un "cran" plus bas en utilisant la pression quantique des neutrons , d'énergie 1836 fois plus petite. la réaction p + e -> n + &nu est endoénergétique et l'energie est fournie par l'effondrement. Il se peut même que les neutrons deviennent relativistes, alors leur distance ne peut être inférieure à d.u.[h, M, c] ce qui donne une taille de l'étoile :

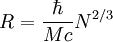
• trou noir : le rayon de Schwarschild R = 2GM²/c² donne la masse de Chandrasekhar , soit N = qq N*, à partir de laquelle l'étoile s'effondre "éternellement au sens relativiste" en un trou noir.

Conclusion

On voit que la notion de Dahus est un peu plus puissante que celle d'A.D. ( analyse dimensionnelle) , car elle permet de mettre en exergue des paramètres non dimensionnels caractéristiques ; ici le nombre d'Avogadro stellaire N* a joué un rôle important, sans lui donner une connotation "numérologique" quelconque.

Voir aussi

• Dahus et Système d'unités naturelles
• Cours Pequignot ( Observatoire de Meudon).
• Cours Stephan Fauve ( ENS-paris)sur les Dahus.