- Symboles de hermann-mauguin
-
Symboles de Hermann-Mauguin
Les symboles de Hermann-Mauguin (ou notation internationale) donnent les éléments de symétrie d'un groupe ponctuel ou d'un groupe d'espace le long de chaque direction de symétrie. Le long d'une direction de symétrie on trouve toujours des éléments de symétrie dans un groupe holohèdre, mais pas toujours dans un groupe mérièdre. Les directions de symétrie sont caractéristiques de chaque système réticulaire.
Système réticulaire première direction de symétrie deuxième direction de symétrie troisième direction de symétrie triclinique --- --- --- monoclinique [010] --- --- orthorhombique [100] [010] [001] tétragonal [001] [100], [010] [110], [1-10] rhomboédrique (axes rhomboédriques) [111] [1-10], [01-1], [10-1] --- rhomboédrique (axes hexagonaux) [001] [100], [010], [110] --- hexagonal [001] [100], [010], [110] [210], [120], [1-10] cubique [001], [100], [010] [111], [1-11], [-111], [-1-11] [110], [1-10], [101], [10-1], [011], [01-1] Symboles de Hermann-Mauguin pour les groupes ponctuels
Le symbole de Hermann-Mauguin d'un groupe ponctuel consiste en les axes parallèles et les miroirs perpendiculaires à chaque direction de symétrie. Lorsque qu'un axe et un miroir coexistent pour la même direction, les deux sont indiqués séparés par un signe de fraction. Par exemple, 2 / m est le symbole de l'holoédrie monoclinique, qui consiste en un axe d'ordre 2 perpendiculaire à un miroir.
Le centre d'inversion, quand il est présent, n'est jamais indiqué sauf dans le système réticulaire triclinique, car soit il est généré par la combinaison d'un axe et d'un miroir (exemple : 2/m ), soit il fait partie d'un axe hélicoïdal (c'est le cas de
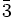).Les symboles de Hermann-Mauguin sont dans la plupart des cas donnés dans leur forme abrégée : lorsque des axes binaires et des miroirs coexistent pour la même direction, il suffit de donner les miroirs, car les axes sont générés par combinaison (exemple : mmm au lieu de 2/m 2/m 2/m ). Exception est le groupe 2/m, car il n'existe qu'une seule direction de symétrie dans le système réticulaire monoclinique.
- Les groupes
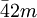et 
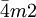diffèrent par l'orientation des axes du référentiel, tournés de 45º. - Les groupes 321 et 312, 3m1 et 31m,
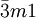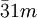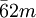et 
, 
et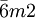 
diffèrent par l'orientation des axes du référentiel, tournés de 30º. - Les groupes 32 et 321, 3m et 3m1,
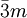et 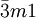diffèrent par leur réseau. 32, 3m et 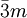est la notation rhomboédrique (il n'existe pas de troisième direction de symétrie dans le système réticulaire rhomboédrique), 321, 3m1 et 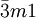est la notation hexagonale (la troisième direction de symétrie dans le système réticulaire hexagonal existe, mais elle n'est pas occupée par des éléments de symétrie dans ces trois groupes).
Symboles de Hermann-Mauguin pour les groupes d'espace
Par rapport à la notation des groupes ponctuels, celle des groupes d'espace présente deux différences principales:
- le symbole contient, en première position, le mode de réseau (P, A, B, C, I, F, R ) ;
- le symbole peut contenir des axes hélicoïdaux ou des miroirs translatoires.
Dans un groupe d'espace, différents éléments de symétrie de la même dimensionalité peuvent co-exister en orientation parallèle. Dans le symbole du groupe d'espace, le choix de l'élément représentatif suit une priorité, qui est la suivante :
- les axes sans glissement ont priorité sur les axes hélicoïdaux ;
- la priorité dans le choix du miroir représentatif est : m > e > a > b > c > n > d.
Voir aussi
- Famille cristalline
- Groupe ponctuel de symétrie
- Groupe d'espace
- Système réticulaire
- Réseau de Bravais
Catégorie : Cristallographie - Les groupes
Wikimedia Foundation. 2010.
