- Stéradian
-
Le stéradian (symbole : sr) est l'unité dérivée du système international pour la mesure d'angles solides.
Sa définition est similaire à celle du radian qui mesure les angles plans. Son nom est partiellement dérivé du grec ancien στερεός (stereos) « solide, dur, cubique ».
Sommaire
Définition
Représentation d'un angle solide valant 1 stéradian.
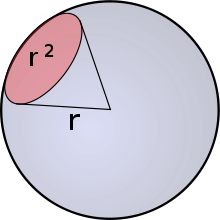
Le stéradian est défini comme étant l'angle solide qui, ayant son sommet au centre d'une sphère, découpe, sur la surface de cette sphère, une aire équivalente à celle d'un carré dont le côté est égal au rayon de la sphère.
Autrement dit, un angle solide d'un stéradian délimite sur la sphère unité à partir du centre de cette sphère une surface d'aire 1. Pour une sphère complète, l'angle solide vaut donc 4π stéradians, la surface d'une sphère complète de rayon r valant 4π r2.
Le stéradian est une unité sans dimension.
Le stéradian fut à partir de 1960 avec le radian une unité SI supplémentaire, mais cette catégorie fut abolie du système international en 1995.
Exemples
- Le regard d'un œil humain embrasse environ 0,5 sr ;
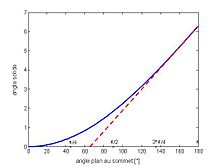
- Un cône circulaire, de demi-angle au sommet θ découpe dans l'espace un angle solide de 2π (1 - cosθ). Pour faciliter ce passage du plan à l'espace, on propose une illustration. Si on met en rotation un angle plan (2θ) de 1,144 radian (65,54°) autour de sa bissectrice, il engendre un cône qui définit un angle solide de 1 stéradian.
Relation d'angle plan à angle solide.- On peut montrer que le développement d'un cône circulaire correspondant à un stéradian fait environ 195°[1].
Formules sur la lumière
Article connexe : Photométrie.Le lumen est l'unité de flux lumineux correspondant au flux émis par une source d'une intensité lumineuse de 1 candela contenu dans un angle solide de 1 stéradian.
Expressions contenant le stéradian :
Avec :
- lm : lumen qui est l'unité de mesure du flux lumineux ;
- sr : stéradian qui est l'unité de mesure d'angle solide ;
- cd : candela qui est l'unité de mesure d'intensité lumineuse ;
- lx : lux qui est l'unité de mesure d'Éclairement lumineux.
Notes et références
- La démonstration se fait en s'intéressant au cercle à l'intersection entre le cône et la sphère. Si le cône a un demi-angle au sommet θ, la circonférence de ce cercle est 2π r sinθ. Comme on s'intéresse à un cône tel que 2π (1 - cosθ) = 1 (stéradian), on peut calculer le sinθ en utilisant la relation sin²θ + cos²θ = 1. La circonférence du disque dont on se sert pour développer le cône fait 2π r, on n'en prendra que la partie 2π r sinθ (comme dans un diagramme circulaire).
Voir aussi
Articles connexes
Catégories :- Unité dérivée du SI
- Unité d'angle
Wikimedia Foundation. 2010.
