Stratège R et K

Le modèle évolutif r/K est une théorie qui explique que l'évolution de la stratégie de reproduction des espèces, est reliée aux fluctuations de l'environnement. Il a été proposé par les écologues Robert MacArthur et E. O. Wilson, en 1967, à partir de leur travail de biogéographie insulaire. Ce modèle est devenu classique et a donné naissance aux concepts d'espèce à stratégie r et espèce à stratégie K (par convention, on utilise exclusivement un « r » minuscule et un « K » majuscule).

C'est une variante plus complexe du classique modèle logistique proposé par Pierre François Verhulst. Cela permet d'introduire l'impact de l'évolution de l'environnement dans la dynamique, en utilisant deux paramètres (« r » et « K ») au lieu d'un seul.

Sommaire 1 Impact de la stabilité de l'environnement sur les stratégies r ou K 2 Description mathématique des deux stratégies 3 Colonisation d'un nouveau milieu 4 r/K, un spectre continu 5 Articles connexes 6 Références

Impact de la stabilité de l'environnement sur les stratégies r ou K

Dans les environnements instables et variables dans le temps, il y a peu d'avantages à être parfaitement adapté à une situation donnée (puisqu'elle va changer). En revanche il est avantageux de pouvoir se reproduire le plus rapidement possible, pour profiter des bonnes conditions lorsqu'elles se représenteront, avant que ces conditions disparaissent. Inversement, lorsque l'environnement est stable, ou avec des variations prévisibles comme des saisons régulières, les espèces le mieux adaptées seront celles qui exploiteront le mieux les ressources, sans pour autant se reproduire rapidement, puisque les ressources sont de toute manière limitées.

Il se dégage ainsi deux stratégies typiques :

• la stratégie r, basée sur la production d'un grand nombre de jeunes, le plus tôt possible, et une mortalité très élevée. C'est une adaptation aux milieux instables et imprévisibles. C'est le cas des micro-organismes qui sont soumis à ce genre de conditions à cause de leur taille.
• la stratégie K, basée sur une durée de vie très longue, et une reproduction rare et tardive.

Description mathématique des deux stratégies

Ce modèle décrit l'évolution d'une population comme une dynamique régie par la règle suivante : "la variation de la population est proportionnelle à son niveau actuel et à l'écart relatif entre ce niveau actuel et le niveau maximum". Cela se traduit mathématiquement par l'équation différentielle suivante :

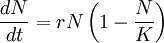
• N est la population,
• r est son taux de croissance,
• et K est la valeur limite de la population, dans les conditions données.

Pour visualiser, on peut observer que :

• lorsque N = K, la population reste constante, quel que soit le niveau du paramètre r;
• lorsque N < K, la population croît à une vitesse proportionnelle à r et à son niveau actuel;
• lorsque N > K, la population décroît à une vitesse proportionnelle à r et à son niveau actuel.

Si K est fixe, ce modèle est rigoureusement le même que celui du modèle de Verhulst, auquel il se ramène par un simple changement de variable A = N/K, avec le même paramètre r. L'idée du modèle, c'est au contraire de considérer K comme variable, et de faire intervenir explicitement le paramètre N/K qui représente l'adaptation de l'espèce aux conditions du moment.

Il ne s'agit que d'un modèle, mais il permet de caractériser les stratégies en œuvre dans le monde réel.

Colonisation d'un nouveau milieu

Lorsqu'un milieu a subi une perturbation (éruption volcanique, grand feu, inondation, stérilisation, ...), les espèces à stratégie r sont les premières à s'implanter, puis elles donnent naissance à un environnement de plus en plus compétitif où les espèces à stratégie K s'imposent. Certains espèces n'auraient même aucune chance de subsister dans la biosphère sans ces catastrophes. Cela définit les successions écologiques d'un écosystème perturbé.

r/K, un spectre continu

Comme toujours en pratique, les êtres vivants appliquent en général une stratégie reproductive intermédiaire entre ces deux extrêmes écologiques. Les arbres et les poissons dispersent ainsi des quantités énormes de rejetons, dont très peu pourront effectivement se reproduire, sans que cela soit incompatible avec l'existence et même la domination locale d'individus très âgés. C'est que la « stabilité » de l'environnement reste très relative, l'espace où s'exerce l'approvisionnement et la vie d'un arbre peut être stable alors que l'espace où s'exerce sa fonction reproductive est beaucoup plus étendu et beaucoup plus aléatoire.

Articles connexes

• Adaptation
• J. Philippe Rushton et son application (controversée) de ce modèle aux races humaines

Références

• MacArthur, R. and Wilson, E. O. (1967). The Theory of Island Biogeography, Princeton University Press (2001 reprint), ISBN 0-691-08836-5
• Pianka, E. R. (1970). On r and K selection. American Naturalist 104, 592-597.
• Pierre François Verhulst (1838). Notice sur la loi que la population poursuit dans son accroissement. Corresp. Math. Phys. 10, 113-121.

• Portail de l’origine et de l’évolution du vivant