Stationnarite d'une serie temporelle

Stationnarité d'une série temporelle

Une des grandes questions dans l'étude de séries temporelles (ou chronologiques) est de savoir si celles-ci suivent un processus stationnaire. On entend par là le fait que la structure du processus sous-jacent supposé évolue ou non avec le temps. Si la structure reste la même, le processus est dit alors stationnaire.

Sommaire

1 Définition forte de la stationnarité
2 Définition faible de la stationnarité
3 Importance de la notion
4 Types de non-stationnarité
- 4.1 Stationnarité en tendance
- 4.2 Stationnarité en différence
  - 4.2.1 Ordre d'intégration d'une série temporelle
5 Tests de stationnarité
- 5.1 Tests de stationnarité
- 5.2 Tests de racine unitaire
6 Références
7 Voir aussi

Définition forte de la stationnarité

Définition — Soit un processus temporel à valeurs réelles et en temps discret 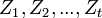$\textstyle Z_1,Z_2,...,Z_t$ . Il est dit stationnaire au sens fort si pour toute fonction f mesurable: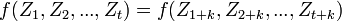

$\textstyle f(Z_1,Z_2,...,Z_t) = f(Z_{1+k}, Z_{2+k}, ..., Z_{t+k})$

Interprétation:

On s'intéresse ici à la distribution conjointe de probabilité du processus. La fonction de densité jointe est-elle la même que l'on prenne les t premières variables ou que l'on prenne les t+k suivantes? Si oui, le processus est alors stationnaire au sens strict. Autrement dit, si le processus est stationnaire, ses propriétés ne sont pas affectées par un changement de notre "repère temporel": que l'on regarde au point t ou au point t+k la série aura toujours le même comportement.

Comme la loi de probabilité d'une distribution d'une série de données est très difficile à estimer, une définition moins stricte de la stationnarité a été introduite.

Définition faible de la stationnarité

Définition — Soit un processus temporel à valeurs réelles et en temps discret 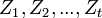$\textstyle Z_1,Z_2,...,Z_t$ . Il est dit stationnaire au sens faible (ou "de second ordre", ou "en covariance") si

$E[Z_i] = \mu \qquad \qquad \qquad \qquad \forall i= 1...t$
$Var[Z_i] = \sigma^2 \ne \infty \qquad \qquad \forall i= 1...t$
$\textstyle Cov[Z_i, Z_{i-k}] = f(k) = \rho_k \qquad \forall i= 1...t, \quad \forall k= 1...t$

Interprétation:

La première condition stipule que l'espérance est constante au cours du temps, il n'y a donc pas de tendance.
La seconde condition stipule que la variance est constante au cours du temps et non infinie.
Troisième condition: L'auto-corrélation (ou auto-covariance, la distinction étant peu importante ici) 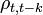$\textstyle \rho_{t,t-k}$ entre la variable 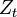$\textstyle Z_t$ et la variable 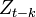$\textstyle Z_{t-k}$ dépend-elle seulement de l'ampleur d'un décalage de k (on a: 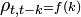$\textstyle \rho_{t,t-k} \scriptstyle = f(k)$ ), ou alors la position dans le temps t joue-t-elle aussi un rôle (alors 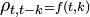$\textstyle \rho_{t,t-k} \scriptstyle = f(t,k)$ )? Si la position dans le temps ne joue pas de rôle alors la série est dite stationnaire au sens faible. On remarquera que la troisième condition inclut la deuxième si l'on prend k=0, et donc l'auto-covariance correspond à la variance.

Importance de la notion

La notion de stationnarité est importante dans la modélisation de série temporelles, le problème de régression fallacieuse montrant qu'une régression linéaire avec des variables non-stationnaires n'est pas valide. Plus précisément, la distribution des paramètres de la régression ne suit plus une loi de Student mais un mouvement brownien. Dans le cas où les variables ne sont pas stationnaires, un concept très proche, celui de coïntégration (en), permet de déterminer le type de modèle à utiliser.

La stationnarité joue également un rôle important dans la prédiction de séries temporelles, l'intervalle de prédiction étant différent selon que la série est stationnaire ou non.

Types de non-stationnarité

Lorsqu'une ou plus des conditions de stationnarité n'est pas remplie, la série est dite non-stationnaire. Ce terme recouvre cependant de nombreux types de non-stationnarité, dont deux sont ici exposés.

Stationnarité en tendance

Définition — Une série est stationnaire en tendance si la série obtenue en "enlevant" la tendance temporelle de la série originale est stationnaire.

La tendance temporelle (ou trend en anglais) d'une série chronologique est sa composante liée au temps.

Exemple: Soit le processus suivant: 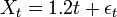$X_{t}=1.2t + \epsilon_t \qquad$ avec $ε t$ un bruit blanc.

Ce processus est non-stationnaire car son espérance augmente avec le temps (condition 1 violée). Mais la série $Y t$ obtenue en soustrayant l'effet de la tendance temporelle, $Y t = X t - 1.2 t$ est stationnaire:

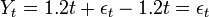$Y_t=1.2t + \epsilon_t -1.2t = \epsilon_t \qquad$ qui est équivalent à un bruit blanc, stationnaire par définition.

Stationnarité en différence

Définition — Une série est stationnaire en différence si la série obtenue en différenciant les valeurs de la série originale est stationnaire.

L'opérateur de différence est noté: $Δ X t = X t - X t - 1$

Ordre d'intégration d'une série temporelle

Définition — Une série temporelle est dite intégrée d'ordre d, que l'on note I(d), si la série obtenue après d différenciations est stationnaire.

Exemple: Soit la marche aléatoire pure: 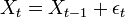$X_{t}=X_{t-1} + \epsilon_t \qquad$ avec $ε t$ un bruit blanc.

On peut montrer qu'une marche aléatoire n'est pas stationnaire. On voit ici qu'elle est intégrée d'ordre 1, la série des différences est en effet stationnaire:

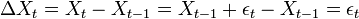$\Delta X_t=X_{t}-X_{t-1}=X_{t-1} + \epsilon_t -X_{t-1}= \epsilon_t\qquad$ équivalent à un bruit blanc, stationnaire par définition.

Tests de stationnarité

Si la fonction de densité n'est pas connue, ce qui est souvent le cas, il est utile de pouvoir déterminer par un test si la série est stationnaire ou non. Il en existe deux types, avec la stationnarité comme hypothèse nulle ou hypothèse alternative:

Tests de stationnarité

L'hypothèse nulle est la stationnarité.

Test KPSS ^[1]

Test de Leybourne et McCabe ^[2]

Tests de racine unitaire

L'hypothèse nulle est la non-stationnarité.

Test de Dickey Fuller (en)^[3]

Test augmenté de Dickey Fuller (en) (ADF)^[4]

Test de Phillips-Perron^[5](PP)

Test DF-GLS (ou ERS) ^[6]

Références

Hamilton (1994), Time Series Analysis, Princeton University Press
Lardic, Mignon (2002), Econométrie des séreis temporelles macroéconomiques et financières, Economica, Paris
Maddala, Kim (1998), Unit roots, Cointegration and Structural Change, Cambridge University Press

↑ Kwiatkowski, D., P.C.B. Phillips, P. Schmidt and Y. Shin (1992), ”Testing the Null Hypothesis of Stationarity against the Alternative of a Unit Root”, Journal of Econometrics, 54, 159-178.
↑ Leybourne, S.J. and B.P.M. McCabe (1994), ”A Consistent Test for a Unit Root”, Journal of Business and Economic Statistics, 12, 157-166
↑ Dickey, D.A. and W.A. Fuller (1979), “Distribution of the Estimators for Autoregressive Time Series with a Unit Root,” Journal of the American Statistical Association, 74, p. 427–431
↑ Said E. and David A. Dickey (1984), 'Testing for Unit Roots in Autoregressive Moving Average Models of Unknown Order', Biometrika, 71, p 599–607
↑ Phillips, Perron (1988) Testing for a Unit Root in a Time Series Regression, Biometrika, 75, p 335-346
↑ Elliott, G., Rothenberg, T., and Stock, J. (1996). Efficient tests for an autoregressive unit root. Econometrica, 64, 813-836

Voir aussi

Portail des probabilités et des statistiques

Ce document provient de « Stationnarit%C3%A9 d%27une s%C3%A9rie temporelle ».

Catégorie : Statistiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Stationnarite d'une serie temporelle de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires: