Règles de bioche

Règles de bioche: Règles de Bioche

Les règles de Bioche, en mathématiques, sont des règles de changement de variable dans le calcul d'intégrales comportant des fonctions trigonométriques. Ces règles ont été inventées par Charles Bioche lorsqu'il était professeur en mathématiques spéciales au lycée Louis-le-Grand. Dans la suite, $f (t)$ est une expression rationnelle en $sin(t)$ et $cos(t)$ , i.e. 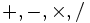une expression obtenue à l'aide de $sin(t)$ , $cos(t)$ , des nombres réels et les quatre opérations $+, -, \times, /$ .

Ainsi, pour calculer
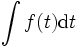$\int f(t)\mathrm{d}t$ ,
on forme $ω(t) = f (t)d t$ . Ensuite,

Si $ω( - t) = ω(t)$ , un changement de variable judicieux est $u (t) = cos(t)$ .

Si $ω(π - t) = ω(t)$ , un changement de variable judicieux est $u (t) = sin(t)$ .

Si $ω(π + t) = ω(t)$ , un changement de variable judicieux est $u (t) = tan(t)$ .

Si 2 des 3 relations précédentes sont vraies (dans ce cas les 3 relations sont vraies), un changement de variable judicieux est $u (t) = cos(2 t)$ .

Dans les autres cas, le changement de variable $u (t) = tan(t / 2)$ s'avère souvent judicieux. On se réferera à ce sujet à l'article sur les formules trigonométriques impliquant la tangente de l'arc moitié

Ces règles ne constituent pas un véritable théorème, mais elles conduisent souvent au bon résultat et permettent le cas échéant de simplifier les calculs. Elles ne sont utilisables dans la plupart des cas que lorsque $f (t)$ comporte des fonctions trigonométriques. Dans le cas où $f$ est une fraction rationnelle en sinus et cosinus les règles de Bioche permettent toujours de se ramener à une primitive de fraction rationnelle qui se calcule aisément par décomposition en éléments simples.

Exemples d’utilisation

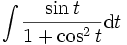Soit l'intégrale $\int \frac{\sin t}{1+\cos^2 t}{\rm d}t$ .
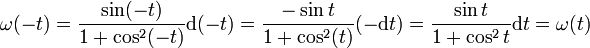
$\omega(-t) = \frac{\sin (-t)}{1+\cos^2 (-t)}{\rm d}(-t)=\frac{-\sin t}{1+\cos^2 (t)}(-{\rm d}t) = \frac{\sin t}{1+\cos^2 t}{\rm d}t = \omega(t)$
(car $d( - t) = - d t$ et $sin$ est impaire et $cos$ paire)

Alors d'après la règle de Bioche, le meilleur changement de variable est $u = cos(t)$ .

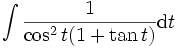Soit l'intégrale $\int \frac{1}{\cos^2 t(1+\tan t)}{\rm d}t$ .
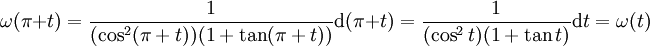
$\omega(\pi+t) = \frac{1}{(\cos^2 (\pi+t))(1+\tan(\pi+t))}{\rm d}(\pi+t)=\frac{1}{(\cos^2 t)(1+\tan t)}{\rm d}t = \omega(t)$
(car $d(π + t) = d t$ et $cos(π + t) = - cos(t)$ et $tan(π + t) = tan(t)$ )

Alors d'après la règle de Bioche, le changement de variable le plus approprié est $u = tan(t)$ .

Une fois le changement de variable effectué, ces deux intégrales peuvent être calculées plus facilement car elles comportent des fonctions que l'on sait primitiver.

Autre version : fonctions hyperboliques

Soit à calculer
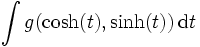$\int{g(\cosh(t), \sinh(t))\,\mathrm{d}t}$ .
Si les règles de Bioche suggèrent de calculer
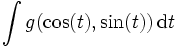
$\int{g(\cos(t), \sin(t))\,\mathrm{d}t}$
par $u = cos(t)$ (resp. $sin(t)$ , $tan(t)$ , $cos(2 t)$ , $tan(t / 2)$ ) un changement de variable judicieux pour la première intégrale est $u = cosh(t)$ (resp. $sinh(t)$ , $tanh(t)$ , $cosh(2 t)$ , $tanh(t / 2)$ ). Dans tous les cas, le changement de variable $u = e t$ permet de se ramener à une primitive de fraction rationnelle, ce dernier changement de variable étant plus intéressant dans le quatrième cas ( $u = tanh(t / 2)$ ).

Voir aussi

Calcul intégral

Calcul numérique d'une intégrale

Intégration par changement de variable

Portail des mathématiques

Ce document provient de « R%C3%A8gles de Bioche ».

Catégorie : Méthode d'intégration

Contenu soumis à la licence CC-BY-SA. Source : Article Règles de bioche de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Regles de Bioche — Règles de Bioche Les règles de Bioche, en mathématiques, sont des règles de changement de variable dans le calcul d intégrales comportant des fonctions trigonométriques. Ces règles ont été inventées par Charles Bioche lorsqu il était professeur… … Wikipédia en Français
Règles de Bioche — En mathématiques, et plus précisément en analyse, les règles de Bioche sont des règles de changement de variable dans le calcul d intégrales comportant des fonctions trigonométriques. Sommaire 1 Les règles et leur justification 2 Exemples… … Wikipédia en Français
Règle de Bioche — Règles de Bioche Les règles de Bioche, en mathématiques, sont des règles de changement de variable dans le calcul d intégrales comportant des fonctions trigonométriques. Ces règles ont été inventées par Charles Bioche lorsqu il était professeur… … Wikipédia en Français
Charles Bioche — Naissance 27 septembre 1859 Dieuze (France) Décès 19 août 1949 (à 89 ans) Ferrières en Brie (France) Nationalité … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Calcul Intégral — Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités … Wikipédia en Français
Calcul Numérique D'une Intégrale — En analyse numérique, il existe toute une famille d algorithmes permettant d approcher la valeur numérique d une intégrale. Toutes consistent à approcher l intégrale par une formule dite de quadrature, du type . Le choix de p, des pondérations ωi … Wikipédia en Français
Calcul integral — Calcul intégral Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités … Wikipédia en Français
Calcul intégral — En mathématiques, plus précisément en analyse, le calcul intégral est l une des deux branches du calcul infinitésimal, l autre étant le calcul différentiel. Sommaire 1 Primitives 1.1 Ensemble des primitives d’une fonction sur un intervalle 2 … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Règles de bioche

Règles de Bioche

Exemples d’utilisation

Autre version : fonctions hyperboliques

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Règles de bioche

Règles de Bioche

Exemples d’utilisation

Autre version : fonctions hyperboliques

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link