Repere log-log
- Repere log-log
-
Repère log-log
Le repère log-log est un repère dans lequel les deux axes sont gradués selon une échelle logarithmique.
Le repère log-log permet de représenter des phénomènes où y est une fonction puissance de x ou, plus généralement, des mesures où x et y peuvent prendre des valeurs proches de 1 et proches de 105
Exemple
Représentation dans un repère log-log de la période de certaines planètes en fonction du demi-grand axe de leur trajectoire (lois de Kepler).
| Planète |
demi grand axe en 109 m |
période en 106s |
| Mercure |
57,9 |
7,58 |
| Vénus |
108,2 |
19,36 |
| Terre |
149,6 |
31,47 |
| Mars |
227,9 |
59,19 |
| Jupiter |
778,3 |
373,32 |
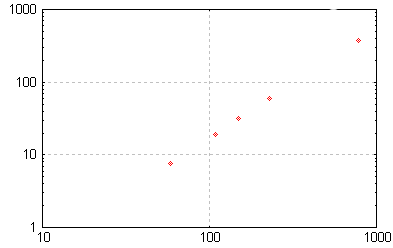Période et demi grand axe dans un repère log-log.
(voir Série statistique à deux variables pour un ajustement de cette droite).
La même série de données en repère cartésien, aurait conduit à un tassement des premiers points pour permettre le placement du dernier point et aurait montré des points se plaçant vaguement sur une courbe polynomiale.
Voir aussi
Repère semi-logarithmique
Portail des mathématiques
Catégorie : Système de coordonnées
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Repere log-log de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Repère log-log — Un repère log log est un repère dans lequel les deux axes sont gradués selon une échelle logarithmique. Un repère log log permet de représenter des phénomènes où y est une fonction puissance de x ou, plus généralement, des mesures où x et y… … Wikipédia en Français
Repere semi-logarithmique — Repère semi logarithmique Un repère semi logarithmique est un repère dans lequel l un des axes, par exemple celui des abscisses (x), est gradué selon une échelle linéaire, comme les graduations d un mètre courant, alors que l autre axe, ici celui … Wikipédia en Français
Repère (mathématiques) — Pour les articles homonymes, voir Repère. En mathématiques, un repère est une collection d éléments de référence permettant de désigner de manière simple n importe quel objet d un ensemble donné. En géométrie, un repère permet de définir les… … Wikipédia en Français
Repère semi-logarithmique — Un repère semi logarithmique est un repère dans lequel l un des axes, par exemple celui des abscisses (x), est gradué selon une échelle linéaire, comme les graduations d un mètre courant, alors que l autre axe, ici celui des ordonnées (y), est… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Logarithme décimal — Représentation graphique du logarithme décimal dans un repère orthogonal Le logarithme décimal ou log10 ou simplement log est le logarithme de base 10. Il est défini en tous les réels strictement positifs x. Le logarithme décimal est la fonction… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Logarithme Décimal — Le logarithme décimal ou log10 est le logarithme de base dix. Il est défini en tous les réels strictement positifs x. Le logarithme décimal est la fonction continue qui transforme un produit en somme et qui vaut 1 en 10. Le logarithme décimal est … Wikipédia en Français
Logarithme decimal — Logarithme décimal Le logarithme décimal ou log10 est le logarithme de base dix. Il est défini en tous les réels strictement positifs x. Le logarithme décimal est la fonction continue qui transforme un produit en somme et qui vaut 1 en 10. Le… … Wikipédia en Français
Échelle logarithmique — Une échelle logarithmique est un système de graduation sur une demi droite [Ox), particulièrement adapté pour rendre compte des ordres de grandeur dans les applications. De plus elle permet de rendre accessible une large gamme de valeurs de même… … Wikipédia en Français
