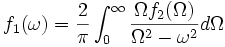Relations de kramers-kronig

Relations de Kramers-Kronig

En mathématiques et physique, les relations de Kramers-Kronig, nommées en l'honneur de Hendrik Anthony Kramers^[1] et Ralph Kronig^[2], décrivent la relation qui existe entre la partie réelle et la partie imaginaire de certaines fonctions complexes. La condition pour qu'elles s'appliquent à une fonction $f (ω)$ est que celle-ci doit représenter la transformée de Fourier d'un processus physique linéaire et causal. Si on écrit

f (ω) = f 1 (ω) + i f 2 (ω)

avec $f 1$ et $f 2$ des fonctions réelles "sympathiques", alors les relations de Kramers-Kronig sont

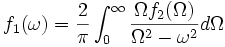
$f_1(\omega) = \frac{2}{\pi} \int_0^{\infty} \frac{\Omega f_2(\Omega)}{\Omega^2 - \omega^2}d\Omega$

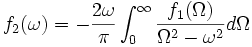$f_2(\omega) = -\frac{2 \omega}{\pi} \int_0^{\infty} \frac{f_1(\Omega)}{\Omega^2 - \omega^2}d\Omega$ .

Les relations de Kramers-Kronig sont liées à la transformée de Hilbert, et sont le plus souvent appliquées à la permittivité $ε(ω)$ des matériaux. Cependant, dans ce cas,

f (ω) = χ(ω) = ε(ω) / ε 0 - 1

avec $χ(ω)$ la susceptibilité électrique du matériau. La susceptibilité peut être interprétée comme la transformée de Fourier de la réponse temporelle du matériau à une excitation infiniment brève, c'est-à-dire sa réponse impulsionnelle.

Notes et références

↑ H.A. Kramers, La diffusion de la lumiere par les atomes, Atti Cong. Intern. Fisica, (Transactions of Volta Centenary Congress) Como, vol. 2, p. 545-557 (1927) .
↑ R. de L. Kronig, On the theory of the dispersion of X-rays, J. Opt. Soc. Am., vol. 12, p. 547-557 (1926).

Voir aussi

Regardez d'autres dictionnaires:

Relations de Kramers-Kronig — En mathématiques et physique, les relations de Kramers Kronig, nommées en l honneur de Hendrik Anthony Kramers[1] et Ralph Kronig[2], décrivent la relation qui existe entre la partie réelle et la partie imaginaire de certaines fonctions complexes … Wikipédia en Français
Kramers–Kronig relation — The Kramers–Kronig relations are mathematical properties, connecting the real and imaginary parts of any complex function which is analytic in the upper half plane. These relations are often used to relate the real and imaginary parts of response … Wikipedia
Kramers-Kronig-Beziehungen — Die Kramers Kronig Beziehungen, auch Kramers Kronig Relation, setzen Real und Imaginärteil bestimmter meromorpher Funktionen in Form einer Integralgleichung miteinander in Beziehung. Sie stellen damit einen Spezialfall der Hilbert Transformation… … Deutsch Wikipedia
Kramers-Kronig-Relation — Die Kramers Kronig Beziehungen (nach Hendrik Anthony Kramers und Ralph Kronig) setzen Real und Imaginärteil bestimmter meromorpher Funktionen in Form einer Integralgleichung miteinander in Beziehung. Sie stellen einen Spezialfall der Hilbert… … Deutsch Wikipedia
Kramers-Kronig-Relationen — Die Kramers Kronig Beziehungen (nach Hendrik Anthony Kramers und Ralph Kronig) setzen Real und Imaginärteil bestimmter meromorpher Funktionen in Form einer Integralgleichung miteinander in Beziehung. Sie stellen einen Spezialfall der Hilbert… … Deutsch Wikipedia
Kramers-Kronig-Transformation — Die Kramers Kronig Beziehungen (nach Hendrik Anthony Kramers und Ralph Kronig) setzen Real und Imaginärteil bestimmter meromorpher Funktionen in Form einer Integralgleichung miteinander in Beziehung. Sie stellen einen Spezialfall der Hilbert… … Deutsch Wikipedia
Kramers-Krönig-Relation — Die Kramers Kronig Beziehungen (nach Hendrik Anthony Kramers und Ralph Kronig) setzen Real und Imaginärteil bestimmter meromorpher Funktionen in Form einer Integralgleichung miteinander in Beziehung. Sie stellen einen Spezialfall der Hilbert… … Deutsch Wikipedia
Ralph Kronig — Ralph de Laer Kronig Naissance 10 mars 1904 Dresde (Allemagne) Décès 16 novembre 1995 (à 91 ans) Zeist ( … Wikipédia en Français
Theorie de la reponse lineaire — Théorie de la réponse linéaire En physique statistique hors d équilibre, la théorie de la réponse linéaire permet de définir les susceptibilités et les coefficients de transport d un système au voisinage de l équilibre thermique indépendamment… … Wikipédia en Français
Théorie de la réponse linéaire — En physique statistique hors d équilibre, la théorie de la réponse linéaire permet de définir les susceptibilités et les coefficients de transport d un système au voisinage de l équilibre thermique indépendamment des détails du modèle. La théorie … Wikipédia en Français

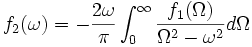Dictionnaires et Encyclopédies sur 'Academic'

Relations de kramers-kronig