Un évènement de réarrangement de génome est un élèment de la dynamique des génomes au cours duquel un génome voit son organisation générale modifiée par le déplacement, la suppression ou la duplication de parties de sa séquence. Les réarrangements de génome couvrent entre autres:

Au sein d'une molécule d'ADN

• Inversion de séquences
• délétions d'une ou plusieurs séquence d'ADN
• la perte d'un bras chromosomique
• les duplications de séquences

Entre molécule d'ADN

• Duplication de chromosome
• Perte de chromosome
• Fusion de deux chromosome par leurs extrémités
• Translocation entre deux chromosomes

Analyse des remaniements chromosomiques entre espèces

Le problème du réarrangement de génomes est un problème de biologie qui peut s'énoncer comme suit : étant donné deux génomes, trouver le nombre minimal de mutations transformant l'un en l'autre. C'est vers la fin des années 1980 que Jeffrey Palmer et ses collègues ont découvert que des organismes très proches au niveau des gènes qu'ils partagent pouvaient néanmoins diverger très fort de par l'ordre dans lequel ces gènes étaient agencés.

Ce problème a également été fort étudié par les mathématiciens et les informaticiens depuis une quinzaine d'années. Parmi les pionniers et les chercheurs les plus prolifiques dans ce domaine, on peut sans aucun doute citer David Sankoff, Vineet Bafna, Sridhar Hannenhalli et Pavel Pevzner. Dans sa forme la plus générale, beaucoup de travail reste à faire, et on a naturellement commencé la recherche par l'étude de formes restreintes du problème, notamment dans le cas où l'on suppose que seul un type de mutation peut se produire. Les mutations étudiées sont entre autres :

• les cassures chromosomiques,
• les inversions ;
• les délétions ;
• les translocations ;
• les transpositions ;
• les fusions ;
• les fissions.

Ainsi que dans certains cas, une combinaison, éventuellement pondérée, de deux ou trois de ces mutations.

Modélisations proposées

Plusieurs modélisations ont été proposées selon le cas dans lequel on se trouve :

• Si l'ordre des gènes est connu et que les génomes étudiés partagent le même nombre et ensemble de gènes sans duplications, on peut les représenter par des permutations et le problème de réarrangement se ramène à un calcul de distance entre permutations. Au moins dans le cas des inversions et des transpositions, les distances ainsi définies sont invariantes à gauche, c'est-à-dire que calculer la distance entre une permutation π et une permutation σ revient au même que de calculer la distance entre la permutation 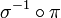et la permutation identité ; d'où l'idée de se ramener au problème de trier une permutation par le nombre minimal d'opérations dont on a fixé le type. Notons au passage que le tri par inversions est NP-difficile, et que la complexité du tri par transpositions est inconnue.
• Si l'on se trouve dans le cas ci-dessus, mais qu'on décide de prendre également en compte l'orientation des gènes, on modélise les génomes par des permutations signées, c'est-à-dire qu'au lieu de considérer des permutations de {1, 2, ..., n}, on considère des permutations de {±1, ±2, ..., ±n}. Un exemple remarquable dans ce cas-ci est le tri par inversions dont la complexité devient polynomiale dans le cas signé alors qu'elle était NP-difficile dans le cas non signé.
• Dans le cas où l'ensemble des gènes est connu mais non leur ordre, on peut recourir à des représentations ensemblistes : les génomes sont vus comme des ensembles non ordonnés de chromosomes, qui sont à leur tour des ensembles non ordonnés de gènes. Ceci ne colle pas avec la réalité : s'il est vrai que les chromosomes ne sont pas ordonnés dans le génome, les gènes sont toujours ordonnés sur un chromosome. Une distance utilisée dans cette modélisation est la distance de synténie (deux gènes sont en synténie s'ils se trouvent sur le même chromosome), qui utilise les opérations de fusion, de fission et de translocation. Ce problème est également NP-difficile.

Voir aussi

• Duplication (génétique)