Raytracing

Exemple d'image de synthèse montrant la réfraction dans 3 milieux différents

Le lancer de rayon (ray tracing en anglais) est une technique de rendu en synthèse d'image simulant le parcours inverse de la lumière de la scène vers l'œil.

Cette technique simple reproduit les phénomènes physiques que sont la réflexion et la réfraction. Une mise en œuvre naïve du lancer de rayon ne peut rendre compte d'autres phénomènes optiques tels que les caustiques (taches lumineuses créées à l'aide d'une lentille convergente par exemple) et la dispersion lumineuse (la radiosité s'attaque à ce problème).

En revanche, contrairement à d'autres algorithmes de synthèse d'image, elle permet de définir mathématiquement les objets à représenter et non pas seulement par une multitude de facettes.

Principe

Le lancer de rayon consiste, pour chaque pixel de l'image générée, à lancer un rayon depuis le point de vue (la caméra) dans la scène 3D. Le premier point d'impact du rayon sur un objet définit l'objet concerné par le pixel correspondant.

Des rayons sont ensuite lancés depuis le point d'impact en direction de chaque source de lumière pour déterminer sa luminosité (est-il éclairé ou à l'ombre d'autres objets ?). Cette luminosité combinée avec la couleur de l'objet ainsi que d'autres informations éventuelles (angles entre la normale à l'objet et les sources de lumières, réflexions, transparence, etc.) déterminent la couleur finale du pixel.

Cette technique fonctionne exactement à l'inverse de la nature, qui, elle, lance des rayons de lumière depuis les sources lumineuses vers l'œil ou la caméra en passant par les objets, alors que le lancer de rayons procède de la caméra vers les sources de lumières. L'expérience montre en effet que cette manière de procéder est nettement plus performante. Pour plus de détails on pourra se reporter à ce travail sur les modèles d'illumination du lancer de rayon.

Différentes techniques permettent d'accélérer ce traitement lourd. Dans le cadre d'objets polygonaux (constitués de triangles par exemple), dessiner l'objet de façon classique (voir rastérisation) permet de déterminer précisément quels pixels seront réellement visibles, et permet de ne lancer de rayons que pour ces pixels limités. Les différentes techniques de détermination des surfaces cachées permettent de la même manière de réduire au maximum le nombre de rayons a lancer. Ces calculs préliminaires peuvent être réalisés par un processeur dédié afin de limiter le traitement à faire faire par le processeur principal. Le raytracing étant très gourmand en calcul vectoriel, l'utilisation de l'accélération matérielle, conçue pour ce calcul vectoriel (Shader), peut grandement aider à optimiser le résultat final.

Exemple du calcul de l'intersection d'un rayon et d'un triangle

Intersection d'un rayon et d'un triangle

Un moyen simple et efficace pour calculer l'intersection d'un rayon avec un triangle consiste à calculer les coordonnées du point d'intersection I dans la base 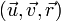. Il suffit de résoudre l'équation vectorielle 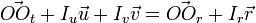. A l'aide de la règle de Cramer, du produit mixte et en posant 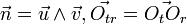on obtient:


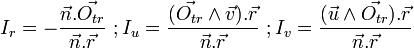
Il suffit ensuite de vérifier que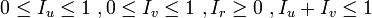
Il est très simple d'étendre cette méthode à des rectangles et même à des polygones grâce au théorème des courbes de Jordan

Futur et prospectives

Cette technique permet la génération d'images très réalistes mais peut requérir un temps de calcul colossal en fonction de la complexité de la scène 3D. Jusqu'en 2001, la puissance des ordinateurs ne permettait pas le calcul d'images en temps réel. Depuis, sous certaines conditions, de nombreuses optimisations de l'algorithme permettent un rendu en temps interactif (quelques images par seconde), voire réellement fluide (au-delà de 25 images par seconde).

L'accélération matérielle par des cartes accélératrices dédiées n'est que très rarement utilisée, mais une interface de programmation existe : OpenRT. Larrabee pourra être utilisé pour accélérer matérialement le rendu par raytracing, mais cette fonctionnalité ne fera pas partie du projet : elle devra être implémentée au besoin par d'autres projets/compagnies.^[1]

Cependant, avec la généralisation des processeurs multi-cœurs l'algorithme du lancer de rayons voit ses possibilités étendues. En effet, cet algorithme se prête particulièrement bien au parallélisme (voir Calcul parallèle), chaque point de l'image pouvant être calculé indépendamment l'un de l'autre. L'immense majorité des logiciels de création graphique basés sur le lancer de rayons utilisent une implémentation multithread permettant la prise en charge des processeurs multi-cœurs. Avec l'apparition de chipsets graphiques multi-cœurs (Larrabee de Intel),ou CUDA de NVIDIA, le lancer de rayons est sans doute amené à prendre de l'importance dans les applications de synthèse d'image en temps réel.

Ces méthodes informatiques pour la prédiction d'images trouvent depuis les années 1990 leurs homologues dans divers domaines, en particulier la prédiction de la propagation d'ondes sonores ou de micro-onde (téléphonie mobile) dans les milieux complexes. Le modèle physique sous-jacent aux algorithmes de lancer de rayon (le principe de Fermat) est en effet commun à l'optique et l'acoustique, à quelques raffinements près liés aux longueurs d'onde manipulées (phénomène de diffraction notamment).

Voir aussi

Liens internes

• Photon mapping
• POV-Ray : un logiciel de lancer de rayons gratuit.
• Yafray : un logiciel de lancer de rayons libre.
• Rayon
• Terragen est un logiciel spécialisé dans les paysages.

Liens externes

• (en) AntiPlanet, un jeu de tir en FPS en temps réel et en lancer de rayon.
• (en) Realstorm, un site avec des benchmarks et un jeu de bowling en démo, en lancer de rayon en temps réel.
• (en) RTChess, un jeu d'échecs en lancer de rayon en temps réel.
• (en) PolyWorld un bench accéléré 3D de RayTracing Temps réel.
• (en) BART une norme de bench accéléré 3D de RayTracing Temps réel, dont le but est la comparaison des mêmes scènes avec du Raycasting.

Notes