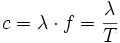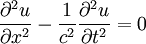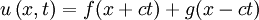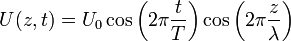Propagation d'une onde

Propagation d'une onde

Propagation des ondes

Page d'aide sur l'homonymie Pour les articles homonymes, voir propagation.

En physique, la propagation des ondes est un phénomène qui est décrit par l'évolution d'une onde, ou du mouvement d'une particule dans le temps et l'espace, par rapport à un milieu. En considérant la direction de propagation de l'onde dans l'espace, on peut distinguer deux types d'ondes :

  • les ondes longitudinales,
  • les ondes transversales.

Le principal paramètre caractérisant la propagation des ondes est la célérité, c'est-à-dire la vitesse de propagation d'une onde dans un milieu donné.

Sommaire

Conditions de propagation

Certains types d'onde ont besoin d'un milieu matériel pour se propager. Par exemple, le son[1] ne se propage pas dans le vide. La propagation d'une onde n'implique pas le déplacement des composants du milieu à grande échelle, mais plutôt leur oscillation. Pour les ondes mécaniques, ce n'est pas la matière qui est transportée, mais l'énergie, on parle alors de « transport d'énergie sans transport de matière ».

Vitesse de propagation

Article détaillé : Vitesse d'une onde.

La vitesse de propagation d'une onde peut être définie comme la vitesse à laquelle la propagation s'effectue, elle vaut :

c = \lambda \cdot f = \frac{\lambda}{T}

où λ est la longueur d'onde et f la fréquence de l'onde.

Équation d'onde

Article détaillé : équation d'onde.

L'équation d'une onde est plus ou moins compliquée suivant le nombre de dimension et le milieu (isotropie, homogénéité) dans lequel elle se déplace. Notamment des termes peuvent intervenir dans l'équation. La solution peut être une fonction scalaire, mais aussi vectorielle, ou tensorielle, ou encore spinorielle.

Une dimension

Le phénomène de propagation des ondes peut être modélisé par une équation d'onde, c'est-à-dire une équation différentielle du second ordre. À une dimension, cette équation est donnée par :

\frac{\partial^2 u}{\partial x^2} - \frac{1}{c^2} \frac{\partial^2 u}{\partial t^2} = 0

et a pour solution :

u\left(x, t\right) = f(x + ct) + g(x - ct)

La solution u(x, t) est une fonction à deux inconnues x et t, mais le problème considéré est bien à une seule dimension spatiale, celle de x, la déformation se fait par rapport à x. La fonction f(x, t) correspond à la propagation de l'onde vers la gauche, et g(x, t) à la propagation vers la droite.

N dimensions

Dans un espace à n dimensions, l'équation d'onde homogène prend la forme :

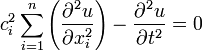c_i^2 \sum_{i=1}^{n} \left( \frac{\partial^2 u}{\partial x_i^2} \right) - \frac{\partial^2 u}{\partial t^2} = 0.

où u = u(x1,...,xn,t) est une solution à n+1 inconnues.

Ondes longitudinales et transversales

On parle d'onde longitudinale lorsque le phénomène physique s'effectue dans la même direction que la propagation de l'onde. Les ondes acoustiques, un système de ressort en sont des exemples. Le terme d'onde transversales est employé lorsque le phénomène physique se fait perpendiculaire à la direction de propagation, comme les ondes électromagnétiques dans le vide, ou les vagues.

Ondes progressives et ondes stationnaires

Articles connexes : onde stationnaire et onde mécanique progressive.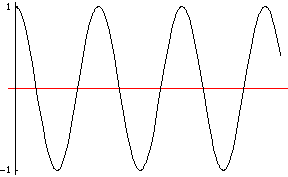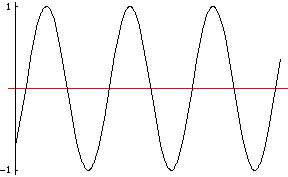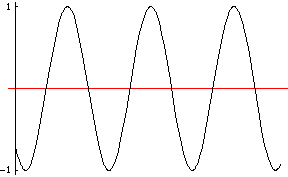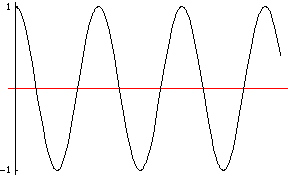
Onde progressive

Il est d'usage dans la communauté scientifique de distinguer les ondes progressives des ondes stationnaires. Les ondes progressives, avancent dans l'espace.

Les ondes stationnaires, au contraire, oscillent sans se déplacer. Ainsi, elles ne dépendent plus du seul paramètre z − ct, mais des paramètres d'espace z et de temps t de façon indépendante. Une expression simple d'une onde stationnaire harmonique à une dimension est la suivante :

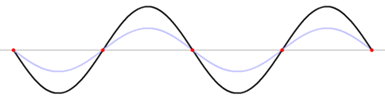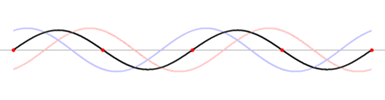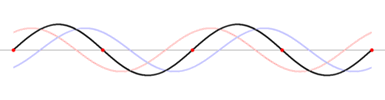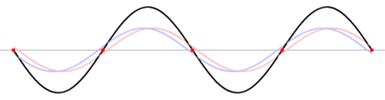U(z, t)=U_0\cos\left(2\pi \frac {t}{T}\right)\cos\left(2\pi \frac {z}{\lambda}\right)
Onde stationnaire

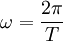
on appele la pulsation \omega = { 2 \pi \over T}

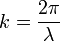
et le vecteur d'onde k = {2 \pi \over \lambda }

À un temps t fixé, une onde stationnaire ressemble à une onde progressive. En revanche, son évolution temporelle est totalement différente. Une onde stationnaire possède des minima (nœuds) et des maxima (ventres) d'amplitude fixes dans l'espace. Ainsi, si on se place aux nœuds de cette onde, l'amplitude est nulle quel que soit le temps. Avec une onde progressive, nous aurions vu l'amplitude évoluer, de façon sinusoïdale avec le temps dans le cas d'une onde harmonique.

Une façon simple de construire une onde stationnaire est de superposer deux ondes progressives se propageant en sens inverse. C'est d'ailleurs ce qui se passe lorsque une onde se réfléchit sur un miroir parfait.

Les ondes stationnaires sont des objets physiques très courants et se rencontrent notamment dans les cavités laser ou les lignes hyperfréquence.

Notes et références

  1. ↑ le son est une onde mécanique qui se propage longitudinalement dans un milieu matériel, la matière.

Voir aussi

Articles connexes

Bibliographie

Lev Landau et Evguéni Lifchitz, Physique théorique, tome 7 : Théorie de l'élasticité, éd. MIR, Moscou [détail des éditions]

Ce document provient de « Propagation des ondes ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Propagation d'une onde de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Vitesse d'une onde — Une onde est une perturbation qui se déplace dans un milieu. Il est possible de lui associer deux vitesses d onde, soit la vitesse de phase et la vitesse de groupe qui, parfois, ne sont pas égales : Dans un milieu homogène, la propagation… …   Wikipédia en Français

  • Démonstration de la formule modélisant une onde sinusoïdale — Une onde sinusoïdale peut se modéliser avec cette formule : Démonstration L’étude de la propagation d’une déformation peut se faire dans deux référentiels, celui du lieu d’observation (Galiléen) xy, ou celui de l’impulsion x’y’. Dans le… …   Wikipédia en Français

  • onde — [ ɔ̃d ] n. f. • XIIe; lat. unda « eau courante » I ♦ 1 ♦ Vx ou littér. Masse d eau qui se soulève et s abaisse en se déplaçant ou en donnant l illusion du déplacement. ⇒ flot, 1. vague. « L onde approche, se brise » (Racine). Fig. « Une onde… …   Encyclopédie Universelle

  • ondé — onde [ ɔ̃d ] n. f. • XIIe; lat. unda « eau courante » I ♦ 1 ♦ Vx ou littér. Masse d eau qui se soulève et s abaisse en se déplaçant ou en donnant l illusion du déplacement. ⇒ flot, 1. vague. « L onde approche, se brise » (Racine). Fig. « Une onde …   Encyclopédie Universelle

  • propagation — [ prɔpagasjɔ̃ ] n. f. • h. XIIIe « descendant »; lat. propagatio, de propagare 1 ♦ (1380) Multiplication par voie de génération. La propagation de l espèce. ⇒ reproduction. « l Église, qui ne voit dans le mariage que la propagation de l humanité… …   Encyclopédie Universelle

  • Onde mecanique progressive — Onde mécanique progressive On appelle onde mécanique le phénomène de propagation de proche en proche d une perturbation locale dans un milieu matériel, sans transport de matière. La caractéristique principale de l onde progressive étant que la… …   Wikipédia en Français

  • Onde mécanique — progressive On appelle onde mécanique le phénomène de propagation de proche en proche d une perturbation locale dans un milieu matériel, sans transport de matière. La caractéristique principale de l onde progressive étant que la perturbation se… …   Wikipédia en Français

  • Onde mécanique progressive — Une onde mécanique progressive est le phénomène de propagation de proche en proche d une perturbation locale dans un milieu matériel, sans transport de matière. La caractéristique principale de l onde progressive étant que la perturbation se… …   Wikipédia en Français

  • Onde mécanique périodique — Onde mécanique progressive On appelle onde mécanique le phénomène de propagation de proche en proche d une perturbation locale dans un milieu matériel, sans transport de matière. La caractéristique principale de l onde progressive étant que la… …   Wikipédia en Français

  • Onde mécanique périodiques — Onde mécanique progressive On appelle onde mécanique le phénomène de propagation de proche en proche d une perturbation locale dans un milieu matériel, sans transport de matière. La caractéristique principale de l onde progressive étant que la… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”