Produit infini de cantor

Produit infini de cantor: Produit infini de Cantor

Construction du produit

Soit $x 0$ un nombre réel strictement plus grand que 1. On définit les nombres suivants, où $\left[ x \right]$ représente la partie entière de x :

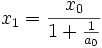$a_0 = \left[ \frac{x_0}{x_0 - 1} \right ]$ , $x_1 = \frac{x_0}{1 + \frac{1}{a_0}}$ .

De ce fait, 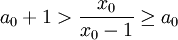$a_0 + 1 > \frac{x_0}{x_0 - 1} \geq a_0$ . Donc, on a $x 1 > 1$ . On peut donc itérer le principe précédent et obtenir :

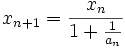$a_n = \left[ \frac{x_n}{x_n - 1} \right ]$ , $x_{n+1} = \frac{x_n}{1 + \frac{1}{a_n}}$ .

Ainsi, on a le théorème suivant : quel que soit x₀ > 1, on peut écrire de manière unique:

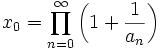$x_0 = \prod_{n=0}^{\infty}{\left(1 + \frac{1}{a_n}\right)}$ .

Propriétés

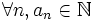
$\forall n, a_n \in \mathbb{N}$

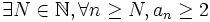
$\exist N \in \mathbb{N}, \forall n \geq N, a_n \geq 2$

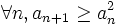
$\forall n, a_{n+1} \geq a_n^2$

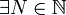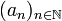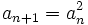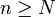Soit $x 0 > 1$ . Alors $x 0$ est un nombre rationnel si, et seulement si, $\exist N \in \mathbb{N}$ tel que la suite $(a_n)_{n \in \mathbb{N}}$ de son développement en série de Cantor vérifie $a_{n+1} = a_n^2$ pour $n \geq N$ .

Exemples

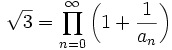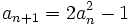$\sqrt{3} = \prod_{n=0}^{\infty}{\left(1 + \frac{1}{a_n}\right)}$ , avec $a 0 = 2$ et $a_{n+1} = 2a_n^2-1$ ,

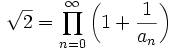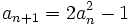$\sqrt{2} = \prod_{n=0}^{\infty}{\left(1 + \frac{1}{a_n}\right)}$ , avec $a 0 = 3$ et $a_{n+1} = 2a_n^2-1$ .

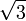D'après les propriétés précédentes, on voit donc que $\sqrt{2}$ et $\sqrt{3}$ sont des nombres irrationnels (même s'il y a beaucoup plus simple pour le démontrer).

L'intérêt premier du développement en produit de Cantor est la rapidité de convergence de l'algorithme, ce qui en fait un candidat intéressant pour une implémentation sur calculatrice.

Portail des mathématiques

Ce document provient de « Produit infini de Cantor ».

Catégories : Série | Georg Cantor

Contenu soumis à la licence CC-BY-SA. Source : Article Produit infini de cantor de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Produit infini de Cantor — Construction du produit Soit x0 un nombre réel strictement plus grand que 1. On définit les nombres suivants, où représente la partie entière de x : , . De ce fait … Wikipédia en Français
Infini — Le symbole infini Le mot « infini » ( e, s ; du latin finitus, « limité »), est un adjectif servant à qualifier quelque chose qui n a pas de limite en nombre ou en taille. Sommaire … Wikipédia en Français
INFINI MATHÉMATIQUE — Le mot «infini» désigne un concept à entrées multiples. Il s’ouvre d’abord sur l’ontologie et signifie alors, selon la tradition, «l’être tel qu’on n’en saurait concevoir de plus grand» («ens quo majus concipi non potest »). Ce fut pour une… … Encyclopédie Universelle
INFINI — La philosophie a emprunté la notion de l’infini – corrélative de la notion du fini – à la réflexion sur l’exercice de la connaissance, d’une part; à l’expérience ou à la tradition religieuse, de l’autre. Ces deux sources déterminent la variété… … Encyclopédie Universelle
Georg Cantor — Pour les articles homonymes, voir Cantor. Georg Cantor Georg Ferdinand Ludwig Philipp Cantor Naissance 3 … Wikipédia en Français
Georg Ferdinand Cantor — Georg Cantor Pour les articles homonymes, voir Cantor. Georg Cantor Georg Ferdinand Ludwig Philipp Cantor … Wikipédia en Français
Georg Ferdinand Ludwig Philipp Cantor — Georg Cantor Pour les articles homonymes, voir Cantor. Georg Cantor Georg Ferdinand Ludwig Philipp Cantor … Wikipédia en Français
George Cantor — Georg Cantor Pour les articles homonymes, voir Cantor. Georg Cantor Georg Ferdinand Ludwig Philipp Cantor … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Produit infini de cantor

Produit infini de Cantor

Construction du produit

Propriétés

Exemples

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Produit infini de cantor

Produit infini de Cantor

Construction du produit

Propriétés

Exemples

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link