- Problème du cavalier
-
Le problème du cavalier (ou encore polygraphie ou algorithme du cavalier) est un problème mathématico-logique fondé sur les déplacements du cavalier du jeu d'échecs (une case en avant puis une case en diagonale dans la même direction). Un cavalier posé sur une case quelconque d'un échiquier doit en visiter toutes les cases sans passer deux fois sur la même.
Sommaire
Histoire
Le cavalier d'Euler est connu depuis fort longtemps. Vers 840, le joueur et théoricien d'échecs arabe al-Adli ar-Rumi en donne déjà une solution. On en trouve la première occurrence dans un traité d'ornement poétique indien, le Kavyalankara du poète Rudrata. Pierre Rémond de Montmort est le premier en occident à avoir étudié ce problème, paru en 1708 dans « Essay d'analyse sur les jeux de hazard » [1]. Puis, le mathématicien Leonhard Euler repris l'étude scientifique en 1759. La « Solution d'une question curieuse qui ne paraît soumise à aucune analyse » n'est cependant publiée qu'en 1766. Côme Alexandre Collini (1727 – 1806), secrétaire de Voltaire en publia une dans le Journal Encyclopédique en 1773.
Parmi les milliards de solutions, seules 122 000 000 se terminent à un pas de la case de départ.
Le problème du cavalier est un cas particulier des graphes hamiltoniens dans la théorie des graphes.
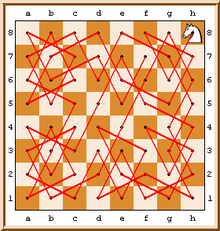
Voici une solution qui permet de parcourir toutes les cases et de revenir à la case de départ, dite fermée.
B1 A3 C2 A1 B3 C1 A2 B4 D5 E7 F5 H4 F3 H2 F1 G3 H1 F2 H3 G1 E2 D4 B5 D6 E8 G7 E6 D8 C6 A7 C8 B6 A8 C7 A6 B8 D7 E5 G4 E3 D1 B2 D3 E1 G2 F4 H5 F6 G8 H6 F7 H8 G6 F8 H7 G5 E4 D2 C4 A5 B7 C5 A4 C3 et retour en B1
La représentation graphique de ce parcours décrit une arabesque.
Au fil des siècles, les mathématiciens étudient ce thème en variant :
- les dimensions de l'échiquier,
- le nombre de joueurs,
- la façon dont un cavalier se déplace.
Au XXe siècle, le groupe d'écrivains Oulipo utilise ce problème. L'exemple le plus remarquable est le tour 10x10 qui détermine l'ordre des chapitres dans le livre de Georges Perec : La Vie mode d'emploi. Il a également utilisé par le même auteur un 9x9 dans Deux cent quarante-trois cartes postales en couleurs véritables.
Pour réussir un parcours sur un damier , il suffit de choisir pour chaque nouveau saut la case libre offrant le moins de sauts ultérieurs possibles : c'est un exercice classique de programmation.
Variante : le tour de cavalier
Dans cette variante, le cavalier doit revenir sur sa case de départ à la fin de son circuit et fait donc une boucle en ne passant qu'une seule fois sur chaque case.
Les tours de cavaliers peuvent se faire sur des damiers de différente taille et sur des formes différentes (rectangle, cube, pavé, spirale infinie, etc.), mais il est nécessaire que le nombre de cases soit pair.
Le tour de cavalier ne peut pas être réalisé sur un damier de moins de 6 cases de côté. C'est une conséquence du théorème qui suit :
Théorème de Schwenk
Pour tout échiquier m × n tel que m soit inférieur ou égal à n, il existe un tour du cavalier, à moins qu'une des conditions suivantes (ou plus) ne soit vraie :
- m et n sont impairs; m et n ne valent pas 1 tous les deux.
- m = 1, 2, ou 4 ; m et n ne valent pas 1 tous les deux.
- m = 3 et n = 4, 6 ou 8.
Condition 1
La condition 1 empêche l'existence d'un tour fermé, pour de simples raisons de parité et de coloriage. Sur un échiquier noir et blanc standard, un cavalier se déplace du blanc vers le noir ou inversement. Donc un tour fermé doit visiter le même nombre de cases noires et blanches, et le nombre des cases visitées doit être pair. Or si m et n sont impairs, le nombre de cases est impair donc aucun tour fermé n'existe. Par contre il peut exister des tours ouverts.
Condition 2
Selon cette condition, il n'existe pas de tour fermé si le plus petit côté est 1, 2, ou 4.
Si m = 1 ou 2, le cavalier ne peut pas atteindre toutes les cases (sauf dans le cas trivial 1 × 1). On peut aussi montrer l'absence de tour fermé dans le cas 4 × n par un argument de coloriage.
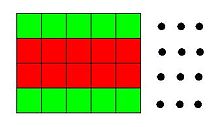
Supposons qu'il existe un tour fermé sur un échiquier 4×n. Appelons A1 l'ensemble des cases noires et A2 l'ensemble des cases blanches visitées par le tour, sur un échiquier noir et blanc standard. Regardons la figure de droite. Appelons B1 les cases vertes et B2 celui des cases rouges. Elles sont en nombre égal. Remarquons que le cavalier passe obligatoirement d'une case de B1 à une case de B2. Comme il doit visiter chaque case, il doit aussi passer d'une case de B2 à une case de B1 (sinon il devrait parcourir deux cases consécutives ou plus de B1 ensuite, ce qui est impossible).
L'examen de ce tour hypothétique donne une contradiction :
- La première case du tour sera dans A1 et B1. Sinon il suffit d'intervertir les définitions de B1 et B2.
- La seconde case doit être dans A2 et B2.
- La troisième case doit être dans A1 et B1.
- La quatrième case doit être dans A2 et B2.
- Et ainsi de suite.
Il en découle que les ensembles A1 et B1 sont confondus, tout comme les ensembles A2 et B2. C'est absurde, donc aucun tour n'existe dans le cas 4 × n, et ce quel que soit n.
Condition 3
On peut prouver la condition 3 au cas par cas. Rechercher un tour fermé dans les cas 3 × 4, 3 × 6, 3 × 8 échoue rapidement. Pour les cas 3 × n, avec n pair et plus grand que 8, on construit les tours fermés par récurrence, en répétant les mouvements.
Autres cas
Nous avons prouvé l'inexistence d'un tour fermé dans les trois conditions mentionnées. Prouver l'existence d'un tel tour dans les autres cas est plus compliqué[2].
Notes et références
- http://gallica.bnf.fr/ark:/12148/bpt6k110519q
- (en) John J. Watkins, Across the Board: the Mathematics of Chessboard Problems, Princeton University Press, 2004 (ISBN 978-0-691-11503-0)
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Knight's tour » (voir la liste des auteurs)
Liens externes
- La description du problème et quelques références par Georges Perec extrait de la revue l'Arc, n°78.
- Une application en Flash pour jouer au problème du cavalier, sur procrastin.fr
- (en) Programme pour résoudre le problème du cavalier, sur le blog de Dmitry Brant
Wikimedia Foundation. 2010.