Problème de napoléon

Problème de Napoléon

En géométrie plane, le problème de Napoléon consiste à construire au compas seul le centre d'un cercle donné. On attribue souvent ce problème et sa démonstration à Napoléon I^er, mais il n'est pas sûr que cette démonstration soit de lui. Certes, il est connu pour son goût pour les mathématiques et sa formation d'artilleur lui permet d'en maîtriser les rouages. Cependant, à la même époque, l'Italien Lorenzo Mascheroni publie sa Géométrie du compas ouvrage dans lequel il étudie justement les constructions au compas seul. Mais au livre dixième, chapitré "des centres" seul le problème 143 qui explique et démontre comment trouver le centre d'un cercle donné, traite la question, et ce de façon très différente de celle dite de Napoléon exposée ici.

Construction

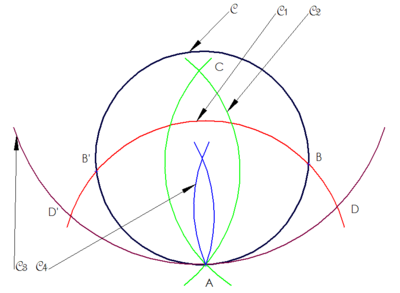
Soit le cercle $\mathcal C$ dont on veut déterminer le centre. Soit un point A de $\mathcal C$ .

Un cercle 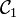$\mathcal C_1$ centré en A rencontre $\mathcal C$ en B et B'.

Deux cercles 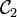$\mathcal C_2$ centrés en B et B' et passant par A se rencontrent au point C.

Un cercle 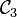$\mathcal C_3$ centré sur C et passant par A rencontre 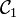$\mathcal C_1$ en D et D'

Deux cercles 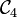$\mathcal C_4$ centrés en D et D' et passant par A se rencontrent au centre de $\mathcal C$ .

Remarque: il est nécessaire, pour que la construction soit réalisable, de prendre pour le rayon du cercle 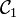$\mathcal C_1$ , une quantité ni trop grande, ni trop petite. Plus précisément, il faut que ce rayon soit compris entre la moitié et le double du rayon du cercle $\mathcal C$ .

Démonstration

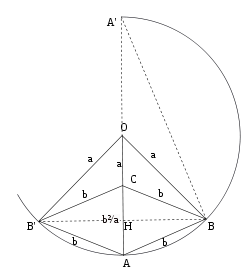
Le principe de la démonstration est la possibilité de construire au compas seul la longueur b²/a si les longueurs a et b sont connues.

La démonstration s'appuie sur les propriétés du triangle rectangle. Dans la figure ci-jointe, le triangle ABA' est rectangle en B et H est le pied de la hauteur issue de B, on peut donc écrire l'égalité suivante :

AH × AA' = AB²

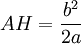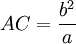
Donc $AH = \frac{b^2}{2a}$ et $AC = \frac{b^2}{a}$

Dans la construction précédente, on retrouve deux fois une configuration de ce type :

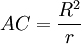
les points A, B et B' sont sur le cercle de centre O et de rayon r, les distances AB, AB', BC et B'C valent R donc $AC = \frac{R^2}{r}$
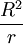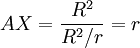les points A, D et D' sont sur le cercle de centre C et rayon $\frac{R^2}{r}$ , les distances DA, D'A, DX, D'X valent R donc $AX = \frac{R^2}{R^2/r}= r$ .

Le point X est bien le centre du cercle (C)

Voir aussi

Portail de la géométrie
Portail du Premier Empire

Ce document provient de « Probl%C3%A8me de Napol%C3%A9on ».

Catégories : Cercle et sphère | Construction géométrique | Napoléon Bonaparte

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Problème de napoléon de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Probleme de Napoleon — Problème de Napoléon En géométrie plane, le problème de Napoléon consiste à construire au compas seul le centre d un cercle donné. On attribue souvent ce problème et sa démonstration à Napoléon Ier, mais il n est pas sûr que cette démonstration… … Wikipédia en Français
Problème de Napoléon — En géométrie plane, le problème de Napoléon consiste à construire au compas seul le centre d un cercle donné. On attribue souvent ce problème et sa démonstration à Napoléon Ier, mais il n est pas sûr que cette démonstration soit de lui. Certes,… … Wikipédia en Français
Napoleon — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte … Wikipédia en Français
Napoleon 1 — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte … Wikipédia en Français
Napoleon Bonaparte — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte … Wikipédia en Français
Napoleon Ier — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte … Wikipédia en Français
Napoléon — Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte … Wikipédia en Français
Napoléon 1 — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte … Wikipédia en Français
Napoléon 1er — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte … Wikipédia en Français
Napoléon Bonaparte — Napoléon Ier « Napoléon » redirige ici. Pour les autres significations, voir Napoléon (homonymie) et Bonaparte … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Problème de napoléon