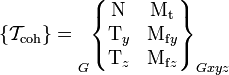Principe de la coupe

Le principe de la coupure, ou principe de la coupe, est un procédé utilisé en résistance des matériaux (mécanique des milieux continus) pour déterminer les contraintes — les efforts de cohésion, ou efforts intérieurs — lorsqu'un objet se déforme.

Principe

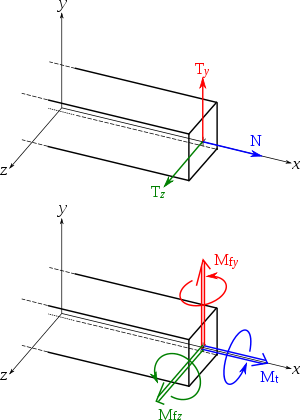
Principe de la coupure pour une poutre encastrée subissant une charge répartie q et une charge concentrée 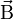à son extrémité libre : le tronçon de gauche (n° 1) exerce une action mécanique 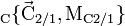sur le tronçon de droite (n° 2), et de manière réciproque, le tronçon 2 exerce une action mécanique 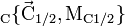sur le tronçon 1

En mécanique, lorsque l'on veut étudier un système, on isole ses composants et on détermine les forces qui s'exercent dessus. Dans le cas des contraintes, il s'agit d'efforts internes s'exerçant entre les atomes de la matière. On effectue donc une opération de pensée dans laquelle on scie l'objet selon un plan donné. On a donc deux objets sur lesquels il faut exercer des forces et couples pour revenir à la situation avant coupure. Les efforts s'exercent sur les sections — les parties sciées —, et sont évidemment symétriques, puisque ce sont les efforts qu'exerce une demi-pièce sur l'autre (principe des actions réciproques).

Supposons un solide à l'équilibre se déformant sous l'effet de deux forces extérieures opposées. Si l'on coupe le solide en deux et que l'on sépare les moitiés, alors chaque moitié n'est soumise qu'à une seule force et donc n'est plus déformée mais mise en mouvement. Pour que chaque moitié retrouve sa déformation, il faut exercer une pression sur chacune des faces de la coupure.

Lorsqu'il y a des symétries évidentes à un problème, le choix de plans de coupe judicieux permet de déterminer de manière simple le tenseur des contraintes. C'est ainsi que l'on peut déterminer que dans le cas de la torsion d'un tube, on a un cisaillement pur.

Conventions de signe

La coupure crée deux tronçons virtuels, notés ci-dessus 1 et 2. On peut définir les efforts de cohésion comme étant :

• l'action du tronçon 2 sur le tronçon 1 ; par rapport au dessin, ces efforts s'exercent à droite de la coupure, on parle donc de la convention des efforts à droite ;
• l'action du tronçon 1 sur le tronçon 2 ; par rapport au dessin, ces efforts s'exercent à gauche de la coupure, on parle donc de la convention des efforts à gauche.

D'après le principe des actions réciproques, ces efforts sont égaux en valeur absolue, mais opposés en signe :

• ,

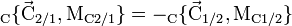on change donc les signes selon la convention que l'on considère.

Si l'on écrit le PFS sur chaque tronçon, on a :

• somme des efforts extérieurs/1 + effort de 2/1 = 0, soit effort de 2/1 = -somme des efforts extérieurs/1 ;
• somme des efforts extérieurs/2 + effort de 1/2 = 0, soit effort de 1/2 = -somme des efforts extérieurs/2 ;

soit

effort de 2/1 = somme des efforts extérieurs/2 et effort de 1/2 = somme des efforts extérieurs/1

On peut donc aussi dire que :

• en convention des efforts à gauche, les efforts de cohésion sont la somme des efforts extérieurs s'exerçant sur le tronçon de gauche ;
• en convention des efforts à droite, les efforts de cohésion sont la somme des efforts extérieurs s'exerçant sur le tronçon de droite.

Cette manière de voir est plus simple à retenir, mais masque le principe de base (le PFS).

Torseur de cohésion

Composantes du torseur de cohésion dans le cas d'une poutre

Comme toutes les action mécaniques, les efforts de cohésion peuvent se décrire par un torseur statique, appelé torseur de cohésion.

Dans le cas d'une poutre d'axe x, ce torseur s'écrit

chaque composante représentant un mode de sollicitation élémentaire :

• N, effort normal : force de direction tangente à la courbe moyenne ;
• T, effort tranchant : force perpendiculaire à la courbe moyenne et provoquant un cisaillement :
  • T_y : effort tranchant selon y,
  • T_z : effort tranchant selon z ;
• M_f, moment fléchissant : moment dont le vecteur est perpendiculaire à la courbe moyenne et provoquant une flexion :
  • M_fy : moment fléchissant selon y,
  • M_fz : moment fléchissant selon z ;
• M_t, moment de torsion : son vecteur a pour direction x.

Exemples

Réservoir cylindrique sous pression

Considérons un réservoir cylindrique de longueur L, de rayon R et d'épaisseur e. La pression du liquide ou du gaz s'exerce de manière homogène, perpendiculairement aux parois.

Si l'on coupe selon un plan contenant l'axe du cylindre, on a deux demi-coques qui sont propulsées par la pression ; pour les « recoller », il faut exercer sur la section une force en direction inverse, donc perpendiculaire à la section, et répartie uniformément. On a donc sur ce plan une contrainte de traction, que l'on peut facilement calculer : on détermine aisément la force qu'exerce la pression sur la demi-coque, ainsi que la surface de la section.

Si l'on coupe selon un plan perpendiculaire à l'axe, il faut de même imposer une force uniforme perpendiculaire à la section pour rapprocher les deux cylindres ouverts.

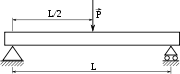
Poutre en flexion

Flexion trois points

Poutre en flexion 3 points

Lorsque l'on coupe la poutre, une partie est soumise à une seule force. Il faut donc exercer une force inverse sur la section pour « immobiliser » la partie, puis un couple pour l'empêcher de tourner ; la force est appelée « effort tranchant » T, le couple est appelé « moment fléchissant » M_f.

L'autre partie est soumise à deux forces inégales, il faut donc de même exercer une force de stabilisation ainsi qu'un moment fléchissant. On retrouve le principe des actions réciproques.

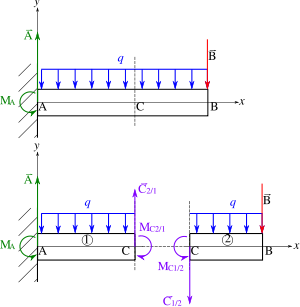
Flexion quatre points

Dans le cas de la flexion quatre points, si l'on exerce une coupure dans la zone centrale, chaque demi-poutre est en équilibre d'un point de vue des forces, mais pas des moments. Les efforts de cohésion se résument donc à un moment fléchissant, on est dans le cas de la « flexion pure ».

Voir aussi