Perles de dijkstra

Les Perles de Dijkstra sont un problème de backtracking en programmation énoncé par Edsger Dijkstra dans les Communications de l'ACM au début des années 1970.

L'intérêt du problème vient du fait qu'il est difficile de le programmer sans instruction GO TO^[1], mais que si on le programme avec une telle instruction, on a de fortes chances aussi de se tromper, et de rendre le programme très dur à corriger.

Il a donné lieu aussi à des développements mathématiques simples.

Sommaire 1 Le problème 2 L'analyse 2.1 Plausibilité 2.2 Familiarisation simple 2.3 Programmation 2.4 Méthode mathématique 3 Références 4 Voir aussi

Le problème

Soit un fil sur lequel on désire enfiler des perles de trois couleurs. Dijkstra propose bleu, blanc et rouge, couleurs du drapeau néerlandais, mais on peut dans une formulation plus neutre les nommer 0, 1 et 2.

Une seule contrainte existe : il ne doit pas y avoir sur le fil deux séquences adjacentes identiques.

Questions :

• Combien de perles peut-on ainsi enfiler ?
• Écrire l'algorithme qui réalise la plus longue séquence possible, ou le cas échéant celui qui pourra continuer indéfiniment.

L'analyse

Plausibilité

Elle commence tout d'abord avec un peu de réflexion préalable : chaque choix de perle est un choix parmi trois. Le degré de liberté dans la construction est de l'ordre de 3^N. La contrainte, elle, semble diminuer plutôt en N^3/2, ce qui conduit à se dire que passé un certain cap, on a assez de marge de manœuvre pour continuer indéfiniment. Mais impression n'est pas démonstration.

Familiarisation simple

Elle contient ensuite avec un peu de simulation à la main :

• 0 est correct
• 00 serait incorrect
• 01 est correct
• 010 est correct
• 0100 et 0101 seraient incorrects
• 0102 est correct
• ...
• 0102010 est correct

Nous avons ensuite un souci pour placer une perle supplémentaire :

• 01020100 ne convient pas (répétition du 0)
• 01020101 ne convient pas (répétition du 01)
• 01020102 ne convient pas davantage (répétition du 0102)

Est-ce la chaîne la plus longue cherchée ? Non. Nous pouvons toujours remettre en cause un de nos choix (arbitraires) antérieurs pour voir si cela ne débloque pas la situation. Et de fait :

0102012 débloque les choses et permet de continuer. Cette procédure se nomme le backtracking.

Il n'y a plus qu'à programmer.

Programmation

Mais attention aux programmeurs négligents : si leur programme ne prévoit pas qu'il puisse y avoir de nombreux backtrackings successifs depuis la même position, ils sont partis pour rencontrer de sérieux ennuis. Ennuis qui deviennent vite inextricables si de surcroît ils ont fait usage de l'instruction GO TO, qui interdit toute prédiction facile sur les invariants valides en chaque point du programme.

Méthode mathématique

On peut construire une telle chaîne arbitrairement longue. Si l'on considère le morphisme 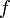(verifiant 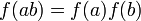) sur l'alphabet 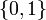vérifian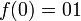t et 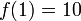et que l'on note 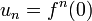. On a alors: 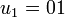; ; 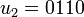; ; 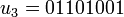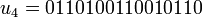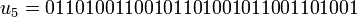. Ainsi l'on défini le mot de Thue et Morse, en prenant la limite de cette suite (car chaque élément de la suite est préfixe des autres). Ce mot possède plusieurs particularités mais ici celle qui nous intéresse ici est la suivante: On remarque que le mot ne comporte jamais de facteur 000 ou 111, ainsi si on factorise la mot en facteur 0.1* et on remplace chacun de ces facteurs par le nombre de 1 qu'il contient (toujours inférieurs a 2). On obtient ainsi le mot: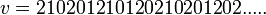

On peut montrer que ce mot est un mot sans facteur carré.

Références

Voir aussi

• backtracking
• branch and bound
• programmation structurée
• recherche opérationnelle
• théorie des graphes

• Portail de l’informatique