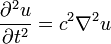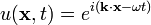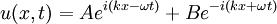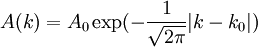Paquet d'ondes

Paquet d'ondes

Paquet d'onde

En physique, un paquet d'onde est une enveloppe ou un paquet contenant un nombre arbitraire de formes d'ondes. En mécanique quantique, le paquet d'onde possède une signification particulière : il est interprété comme étant une onde de probabilité qui décrit la probabilité pour une particule (ou des particules) dans un état donné d'avoir une position et une quantité de mouvement données.
En appliquant l'équation de Schrödinger en mécanique quantique, il est possible de déduire l'évolution temporelle d'un système, de manière similaire au formalisme hamiltonien en mécanique classique. Le paquet d'onde est une solution mathématique de l'équation de Schrödinger. Le carré de l'aire en dessous du paquet d'onde solution (intégrale quadratique) est interprétée comme étant la densité de probabilité de trouver une particule dans cette région.
Dans une représentation à coordonnées d'une onde (comme par exemple en coordonnées cartésiennes), la position de l'onde est donnée par la position du paquet. De plus, plus le paquet d'onde est petit, mieux est définie la position du paquet d'onde, mais plus l'incertitude sur la quantité de mouvement est grande. Cette particularité est connue sous le nom de principe d'incertitude de Heisenberg.

Bases

Au début des années 1900, il devient évident que la mécanique classique montraient des défaillances majeures. Isaac Newton proposa originellement l'idée que la lumière se déplaçait en paquets discrets appelés « corpuscules », mais le comportement ondulatoire de nombreux phénomènes lumineux conduisit les scientifiques à favoriser une description en termes d'ondes de l'électromagnétisme. Ce n'est que dans les années 1930 que la nature particulaire de la lumière commença réellement et largement à être acceptée en physique. Le développement de la mécanique quantique - et son succès dans l'explication de résultats expérimentaux qui pouvaient sembler paradoxaux - fut la base principale de cette acceptation.
Un des concepts les plus importants dans la formulation de la mécanique quantique est l'idée que la lumière se déplace en quantités discrètes appelées photons. L'énergique de la lumière est une fonction discrète de la fréquence :

E = nhf

L'énergie est le produit d'un entier n (d'où le terme de quantification), de la constante de Planck h et la fréquence f. Cette quantification permit la résolution d'un problème de la physique classique, appelé catastrophe ultraviolette.

Les idées de la mécanique quantique continuèrent à être développées tout au long du XXe siècle. L'image qui fut développée fut celle d'un monde particulaire, avec tous phénomènes et toute matière faits de et interagissant avec des particules discrètes. Cependant, ces particules sont décrites par une onde de probabilité. Les interactions, localisations, et toute la physique peuvent être réduits à des calculs de ces ondes d'amplitudes de probabilités. La nature particulaire du monde physique fut confirmée de manière expérimentale, alors que les phénomènes ondulatoires peuvent être caractérisés par la nature en paquets d'ondes des particules.

Mathématiques des paquets d'ondes

Considérons les ondes solutions de l'équation d'onde suivante :

{ \partial^2 u \over \partial t^2 } = c^2 { \nabla^2 u }

où c est la vitesse de propagation de l'onde dans un milieu donné. L'équation d'onde possède des ondes planes comme solutions :

u(\bold{x},t) = e^{i{(\bold{k\cdot x}}-\omega t)}

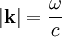où |\bold{k}|=\frac{\omega}{c} . Pour simplifier, considérons que les ondes se déplacent dans une seule dimension. La solution générale est alors :

u(x,t)= A e^{i(kx-\omega t)} + B e^{-i(kx+\omega t)} \,

Un paquet d'onde est une perturbation localisée résultant de la somme de différentes fonctions d'ondes. Si le paquet est très localisé, de nombreuses fréquences sont nécessaires afin de permettre la superposition constructive de la région de la localisation et la superposition destructive hors de cette région. À partir des solutions dans une dimension, une fonction générale d'un paquet d'onde peut être exprimée comme :

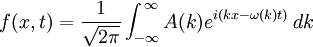f(x,t) = \frac{1}{\sqrt{2\pi}} \int^{\,\infty}_{-\infty} A(k) e^{i(kx-\omega(k)t)} \,dk .

Le 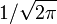1/\sqrt{2\pi} provient des conventions utilisée pour les transformées de Fourier. L'amplitude A(k) contient les coefficients de la superposition linéaire des ondes planes solutions. Ces coefficients peuvent être exprimés comme fonctions de f(x,t) évaluées à t = 0:

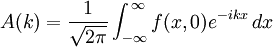A(k) = \frac{1}{\sqrt{2\pi}} \int^{\,\infty}_{-\infty} f(x,0) e^{-ikx}\,dx .

Cette équation différentielle a une solution simple et utile en accord avec la statistique de Maxwell-Boltzmann :

A(k) = A_{0}\exp(-\frac{1}{\sqrt{2\pi}}|k - k_{0}|)

où Ao et ko sont constants.

Référence

  • John David Jackson, Électrodynamique classique [« trad. de (en)Classical Electrodynamics »] 
  • (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Wave packet ».
  • Portail de la physique Portail de la physique
Ce document provient de « Paquet d%27onde ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Paquet d'ondes de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • paquet d’ondes — banginis paketas statusas T sritis fizika atitikmenys: angl. wave packet vok. Wellengruppe, f; Wellenpaket, n rus. волновой пакет, m pranc. paquet d’ondes, m …   Fizikos terminų žodynas

  • extension du paquet d’ondes — bangų paketo išplitimas statusas T sritis fizika atitikmenys: angl. extension of wave packet vok. Ausdehnung des Wellenpackets, f rus. расширение волнового пакета, n pranc. extension du paquet d’ondes, f …   Fizikos terminų žodynas

  • temps de diffusion du paquet d’ondes — bangų paketo išplitimo trukmė statusas T sritis fizika atitikmenys: angl. diffusing time of wave packet vok. Zerfließzeit des Wellenpakets, f rus. время расплывания волнового пакета, n pranc. temps de diffusion du paquet d’ondes, m …   Fizikos terminų žodynas

  • Paquet d'onde — En physique, un paquet d onde est une enveloppe ou un paquet contenant un nombre arbitraire de formes d ondes. En mécanique quantique, le paquet d onde possède une signification particulière : il est interprété comme étant une onde de… …   Wikipédia en Français

  • Paquet d'onde gaussien — Article détaillé : Paquet d onde. Introduction sur les paquets d ondes planes à trois dimensions Dans le cadre de la mécanique quantique, on peut s intéresser à la forme des solutions de l équation de Schrödinger dans le cas d une particule… …   Wikipédia en Français

  • PAQUETS D’ONDES — Terme utilisé en théorie de la propagation des ondes pour désigner une superposition d’ondes, en général planes et monochromatiques, de longueurs d’onde et de directions de propagation voisines. Un paquet d’ondes f (x , t ) se propageant dans une …   Encyclopédie Universelle

  • Dispersion — Pour les articles homonymes, voir Dispersion (homonymie). Dispersion de la lumière blanche au passage d un dioptre. La dispersion, en mécanique ondulatoire, est le phénomène affectant une onde dans un milieu dispersif, c …   Wikipédia en Français

  • Effet Hartman — Lors de la traversée par effet tunnel il peut s avérer que le sommet du paquet d ondes, associé à une particule, apparaisse franchir la barrière de potentiel à une vitesse supérieure à la vitesse de la lumière. L effet Hartman, ainsi nommé parce… …   Wikipédia en Français

  • Dispersif — Dispersion Pour les articles homonymes, voir Dispersion (homonymie). Dispersion de la lumière blanche au passage d un dioptre. La dispersion, en mécanique ondulatoire, est le phénomène affectant une …   Wikipédia en Français

  • Dispersion (optique) — Dispersion Pour les articles homonymes, voir Dispersion (homonymie). Dispersion de la lumière blanche au passage d un dioptre. La dispersion, en mécanique ondulatoire, est le phénomène affectant une …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”