Opérateur normal
- Opérateur normal
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Opérateur normal de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Opérateur monotone — En mathématiques, un opérateur monotone est une multifonction définie entre espaces préhilbertiens, qui possède une propriété de monotonie que nous précisons dans la définition ci dessous. Lorsque cet opérateur est une «simple» fonction réelle d… … Wikipédia en Français
Opérateur adjoint — En mathématiques l adjoint d un opérateur, quand il existe, est un nouvel opérateur défini sur un espace vectoriel sur le corps des nombres réels ou complexes, muni d un produit scalaire. Un tel espace est qualifié de préhilbertien. Si l… … Wikipédia en Français
Opérateur autoadjoint — Endomorphisme autoadjoint En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint est un cas particulier d application linéaire. Cette propriété s applique à une application linéaire d un espace vectoriel dans lui… … Wikipédia en Français
Endomorphisme normal — Un endomorphisme normal est un opérateur d un espace de Hilbert qui commute avec son adjoint. Sommaire 1 Définition 2 Exemples 3 Propriétés 4 Article connexe … Wikipédia en Français
Endomorphisme autoadjoint — En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint ou opérateur hermitien est un endomorphisme d espace de Hilbert qui est son propre adjoint (sur un espace de Hilbert réel on dit aussi endomorphisme… … Wikipédia en Français
Fonction racine carrée — Racine carrée La racine carrée d’un nombre réel positif x est le nombre positif dont le carré vaut x. On le note ou x½. Une tablette d argile datée du XLVIIIe siècle av. J. C. montre que les Babyloniens connaissaient la racine carrée de deux … Wikipédia en Français
Puissance un demi — Racine carrée La racine carrée d’un nombre réel positif x est le nombre positif dont le carré vaut x. On le note ou x½. Une tablette d argile datée du XLVIIIe siècle av. J. C. montre que les Babyloniens connaissaient la racine carrée de deux … Wikipédia en Français
Racine Carree — Racine carrée La racine carrée d’un nombre réel positif x est le nombre positif dont le carré vaut x. On le note ou x½. Une tablette d argile datée du XLVIIIe siècle av. J. C. montre que les Babyloniens connaissaient la racine carrée de deux … Wikipédia en Français
Racine Carrée — La racine carrée d’un nombre réel positif x est le nombre positif dont le carré vaut x. On le note ou x½. Une tablette d argile datée du XLVIIIe siècle av. J. C. montre que les Babyloniens connaissaient la racine carrée de deux et un… … Wikipédia en Français
Racine carree — Racine carrée La racine carrée d’un nombre réel positif x est le nombre positif dont le carré vaut x. On le note ou x½. Une tablette d argile datée du XLVIIIe siècle av. J. C. montre que les Babyloniens connaissaient la racine carrée de deux … Wikipédia en Français
 un espace préhilbertien, réel ou complexe. Soit
un espace préhilbertien, réel ou complexe. Soit 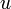 un endomorphisme de
un endomorphisme de  admettant un adjoint
admettant un adjoint 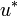 . On dit que
. On dit que 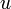 est normal si
est normal si 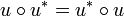 .
.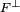 sont à la fois u-stables et u * -stables.
sont à la fois u-stables et u * -stables. ou
ou  espace vectoriel muni d'une norme
espace vectoriel muni d'une norme 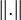 alors
alors 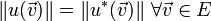 .
.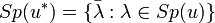 , où
, où 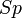 est le spectre de l'application.
est le spectre de l'application.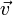 est un vecteur propre de u associé à une valeur propre λ, alors il est un vecteur propre de u * pour la valeur propre
est un vecteur propre de u associé à une valeur propre λ, alors il est un vecteur propre de u * pour la valeur propre 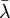 .
.