- Nœud borroméen
-
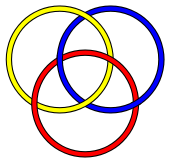
Nœud borroméen
Nœud borroméen standard.
En mathématiques, un nœud borroméen est constitué de trois cercles (au sens topologique) qui sont liés de manière à former un entrelacs brunnien, ce qui signifie qu'enlever l'un quelconque des trois cercles libère les deux autres.
Sommaire
Origine et représentations
Nœud borroméen utilisé comme symbole de la trinité chrétienne, image d'un manuscrit du XIIIe siècle.Le nœud doit son nom de borroméen à l'utilisation qui en était faite dans les armoiries d'une famille italienne, les Borromée. On retrouve néanmoins des nœuds borroméens bien avant cela, comme par exemple dans l'art bouddhique afghan du deuxième siècle de l'ère chrétienne ou dans le symbole du Valknut en Scandinavie au VIIe siècle. Les nœuds borroméens ont été utilisés dans différents contextes pour symboliser la force et l'unité, notamment la religion et les arts. En psychanalyse, c'est par le nœud borroméen que Jacques Lacan choisit de représenter la structure du sujet.
Assimilés au triskell, ils sont aussi parfois représentés comme emblème de l'unité des chevaliers de la table ronde dans les légendes arthuriennes.
Nœuds borroméens ouverts
On retrouve aussi des nœuds borroméens partiels, dans lesquels trois éléments sont entrelacés de même manière que dans le nœud borroméen normal, mais où ces éléments ne sont pas fermés (comme sur la pierre de Snoldelev[1] ou sur l'emblème de Diane de Poitiers).
Réalisation en dimension 3
Anneaux borroméens en dimension 3, vus de face
Anneaux borroméens en dimension 3, vus de profilEn 1987, Freedman et Skora ont prouvé qu'il n'était pas possible de réaliser matériellement un noeud borroméen dans l'espace de dimension 3 à l'aide d'anneaux circulaires[2]. On peut donner l'illusion d'une telle réalisation en utilisant des anneaux courbés, donnant l'impression d'être circulaires lorsqu'ils sont vus sous un certain angle.
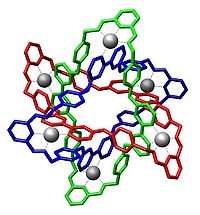
Nœuds borroméens moléculaires
Nœud borroméen moléculaire.Les nœuds borroméens moléculaires sont des architectures moléculaires mécaniquement entrelacées. C'est en 1997 que Chengde Mao et son laboratoire de l'université de New York réussissent à construire un nœud borroméen avec de l'ADN circulaire[3].
Articles connexes
Liens externes
Notes et références
- ↑ en:Snoldelev_Stone
- ↑ M.H. Freedman, R.K.Skora, Strange actions of groups on spheres, J. Differential Geom., 25 (1987) 75-98
- ↑ Nature, vol 386, page 137, Mars 1997.
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Borromean rings ».
Portail des mathématiques
Catégorie : Théorie des nœuds
Wikimedia Foundation. 2010.
