Nombres et supernombres de poulet

Nombres et supernombres de poulet

Nombre et supernombre de Poulet

Un test de primalité courant pour un nombre impair n consiste à tester si n divise 2 n - 2 : dans le cas contraire, en vertu du petit théorème de Fermat, on conclut que n n'est pas premier. Cependant il existe des nombres composés qui passent ce test avec succès : on les appelle nombres pseudopremiers en base 2, ou encore nombres de Poulet, ou, également, nombres de Sarrus.

  • Un nombre composé n est donc un nombre de Poulet si n divise 2 n - 2.
  • Un supernombre de Poulet est un nombre dont chaque diviseur composé est un nombre de Poulet.

Un nombre composé n est donc un nombre de Poulet si tout diviseur d de n divise 2 d - 2. Si un tel diviseur d est composé, d est lui-même un supernombre de Poulet.

Sommaire

Exemples

Par exemple, 341 est un supernombre de Poulet : ses diviseurs positifs sont {1, 11, 31, 341} et on a :

\begin{array}{l} \scriptstyle 2^{11} - 2 \,=\, 11 \times 186\\ \scriptstyle 2^{31} - 2 \,=\, 31 \times 69273666\\ \scriptstyle 2^{341} - 2 \,=\, 341 \times 13136332798696798888899954724741608669335164206654835981818117894215788100763407304286671514789484550 \end{array}

Il est trivial que tous les nombres de Poulet n'ayant que deux facteurs premiers sont des supernombres de Poulet; c'est le cas de 341.

Premiers nombres et supernombres de Poulet

Les premiers nombres et supernombres de Poulet et leur décomposition sont présentés dans les tables qui suivent :

Nombres de Poulet
Nombre Décomposition
341 11 × 31
561 3 × 11 × 17
645 3 × 5 × 43
1105 5 × 13 × 17
1387 19 × 73
1729 7 × 13 × 19
1905 3 × 5 × 127
2047 23 × 89
2465 5 × 17 × 29
2701 37 × 17
2821 7 × 13 × 31
Supernombres de Poulet
Nombre Décomposition
341 11 × 31
1387 19 × 73
2047 23 × 89
2701 37 × 73
3277 29 × 112
4033 37 × 109
4369 17 × 257
4681 31 × 151
5461 43 × 127
7957 73 × 109
8321 53 × 157
Nombres de Poulet pairs
Nombre Décomposition
161038 2 × 73 × 1103
215326 2 × 23 × 31 × 151
2568226 2 × 23 × 31 × 1801
3020626 2 × 7 × 359 × 601
7866046 2 × 23 × 271 × 631
9115426 2 × 31 × 233 × 631
49699666 2 × 311 × 79903
143742226 2 × 23 × 31 × 100801
161292286 2 × 127 × 199 × 3191
196116194 2 × 127 × 599 × 1289 
209665666  2 × 7 × 89 × 197 × 881 

Notez que les supernombres de Poulet présentés ici sont tous des nombres de Poulet à deux facteurs premiers.

Nombres de Poulet à deux facteurs premiers

On l'a vu, les nombres de Poulet à deux facteurs premiers sont des supernombres de Poulet.

On peut également les caractériser comme suit : Soient p et q deux nombres premiers ; leur produit pq est un nombre de Poulet si, et seulement si, q divide 2p - 2 et p divise 2q - 2.


Preuve (utilise le formalisme de l'arithmétique modulaire)

Reformulons le résultat avec le formalisme de l'arithmétique modulaire :

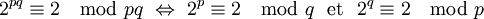
2^{pq} \equiv 2 \mod pq \ \Leftrightarrow\ 2^p \equiv 2 \mod q\ \text{ et }\ 2^q \equiv 2 \mod p

Rappelons que le petit théorème de Fermat assure que

2^p \equiv 2 \mod p
2^q \equiv 2 \mod q

On a donc

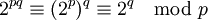
2^{pq} \equiv (2^p)^q \equiv 2^q \mod p
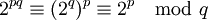
2^{pq} \equiv (2^q)^p \equiv 2^p \mod q

D'autre part, p et q étant premiers, par une application simple du théorème des restes chinois, on a l'équivalence suivante :

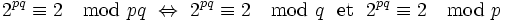
2^{pq} \equiv 2 \mod pq \ \Leftrightarrow\ 2^{pq} \equiv 2 \mod q\ \text{ et }\ 2^{pq} \equiv 2 \mod p

La conclusion est maintenant immédiate.

Supernombres de Poulet à plus de deux facteurs premiers

On peut construire des supernombres de Poulet à trois facteurs premiers de la façon suivante :

  • si p1 , p2 , p3 sont trois nombres premiers distincts tels que p1 p2 , p1 p3 , et p2 p3 sont des supernombres de Poulet, alors p1 p2 p3 est un supernombre de Poulet.

Par exemple, il est facile de lire dans le tableau ci-dessus que les nombres premiers 37, 73 et 109 conviennent. Leur produit : 294409 = 37×73×109 est un supernombre de Poulet.

On a également la généralisation suivante :

  • Si p1 , p2 ,..., pn sont n nombres premiers distincts tels que tous les produits pi pj (avec i différent de j) sont des supernombres de Poulet, alors le produit p1 p2 ... pn est un supernombre de Poulet.



Preuve (utilise le formalisme de l'arithmétique modulaire)

D'après la caractérisation donnée plus haut pour les nombres de Poulet à deux facteurs premiers, l'hypothèse peut se reformuler ainsi :

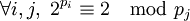
\forall i,j,\ 2^{p_i} \equiv 2 \mod {p_j}

(pour i = j, c'est le petit théorème de Fermat.)

La preuve est par récurrence sur n.

Commençons par le cas n = 3. Les diviseurs composés stricts de 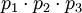p_1\cdot p_2\cdot p_3 sont des nombres de Poulet par hypothèse. Il reste à montrer que 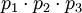p_1\cdot p_2\cdot p_3 également.

On a

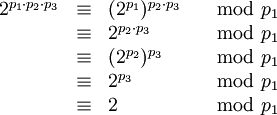
\begin{array}{rcll} 2^{p_1\cdot p_2\cdot p_3} &\equiv& (2^{p_1})^{p_2\cdot p_3} &\mod p_1\\ &\equiv& 2^{p_2\cdot p_3} &\mod p_1\\ &\equiv& (2^{p_2})^{p_3} &\mod p_1\\ &\equiv& 2^{p_3} &\mod p_1\\ &\equiv& 2 &\mod p_1\\ \end{array}

Les pi jouant un rôle symmétrique, on a de la même façon

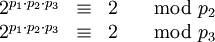
\begin{array}{rcll} 2^{p_1\cdot p_2\cdot p_3} &\equiv& 2 &\mod p_2\\ 2^{p_1\cdot p_2\cdot p_3} &\equiv& 2 &\mod p_3\\ \end{array}

Les pi étant des nombres premiers distincts, on en conclut que

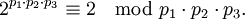
2^{p_1\cdot p_2\cdot p_3} \equiv 2 \mod p_1\cdot p_2\cdot p_3.

Ceci conclut le cas n = 3.

Passons au cas général. L'hypothèse de récurrence entraîne de façon immédiate que tous les diviseurs composés stricts de 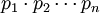p_1\cdot p_2\cdots p_n sont des nombres de Poulet. Il reste à vérifier que 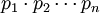p_1\cdot p_2\cdots p_n est lui-même un nombre de Poulet. La preuve faite dans le cas n = 3 est facilement généralisable.

Sept, huit facteurs premiers, et plus encore

Les familles de nombres premiers qui suivent permettent d'obtenir des nombres de Poulet avec jusqu'à sept facteurs premiers distints :

  • 103, 307, 2143, 2857, 6529, 11119, 131071
  • 709, 2833, 3541, 12037, 31153, 174877, 184081
  • 1861, 5581, 11161, 26041, 37201, 87421, 102301 (*)
  • 6421, 12841, 51361, 57781, 115561, 192601, 205441

Ces familles ci permettent d'aller jusqu'à huit facteurs premiers distincts :

  • 1861, 5581, 11161, 26041, 37201, 87421, 102301, 316201 (*)
  • 2383, 6353, 13499, 50023, 53993, 202471, 321571, 476401
  • 2053, 8209, 16417, 57457, 246241, 262657, 279073, 525313
  • 1801, 8101, 54001, 63901, 100801, 115201, 617401, 695701

Notez la parenté entre les deux lignes marquées (*) ci-dessus ! Cette liste de nombres premiers peut en fait être poursuivie jusqu'à vingt-deux nombres premiers disctincts :

  • 1861, 5581, 11161, 26041, 37201, 87421, 102301, 316201, 4242661, 52597081, 364831561, 2903110321, 8973817381, 11292210661, 76712902561, 103410510721501, 29126056043168521, 3843336736934094661, 24865899693834809641, 57805828745692758010628581, 9767813704995838737083111101, 934679543354395459765322784642019625339542212601

Facteurs carrés

Il existe aussi des supernombres de Poulet qui ont des facteurs carrés : en particulier, les carrés des nombres de Wieferich. On peut définir les nombres de Wieferich comme des nombres premiers p tels que p2 est un supernombre de Poulet ; on n'en connait que deux, p = 1093 et p = 3511. Ainsi, 10932 , 35112 sont des supernombres de Poulet, mais aussi 10932 × 4733, et d'autres.

Nombres de Poulet pairs

On connait des nombres de Poulet pairs ; le plus petit d'entre eux, 161038 = 2 × 73 × 1103, a été découvert par Derrick Lehmer en 1950.

Il est par ailleurs assez facile de démontrer qu'il n'y a pas de supernombres de Poulet pairs. En effet, un tel nombre admettrait un diviseur composé de la forme 2p avec p premier, qui serait un nombre de Poulet. Or

22p − 2 = (2p − 2)(2p + 2) + 2.

Si c'est un nombre de Poulet, il est divisible par 2p: on en déduit que

p divise (2p − 2)(2p − 1 + 1) + 1.

Or, d'après le petit théorème de Fermat, p divise (2p − 2). On a alors p divise 1, ce qui est absurde. Il n'existe donc pas de nombre de Poulet de la forme 2p avec p premier, et a fortiori pas de supernombre de Poulet pair.

Liens externes et sources

Sur l'encyclopédie électronique des suites entières de Sloane on trouve :

Cette page (en anglais) donne beaucoup d'informations sur les nombres et supernombres de Poulet :

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre et supernombre de Poulet ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombres et supernombres de poulet de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Nombres Et Supernombres De Poulet — Nombre et supernombre de Poulet Un test de primalité courant pour un nombre impair n consiste à tester si n divise 2 n 2 : dans le cas contraire, en vertu du petit théorème de Fermat, on conclut que n n est pas premier. Cependant il existe… …   Wikipédia en Français

  • Nombres et supernombres de Poulet — Nombre et supernombre de Poulet Un test de primalité courant pour un nombre impair n consiste à tester si n divise 2 n 2 : dans le cas contraire, en vertu du petit théorème de Fermat, on conclut que n n est pas premier. Cependant il existe… …   Wikipédia en Français

  • Supernombres de Poulet — Nombre et supernombre de Poulet Un test de primalité courant pour un nombre impair n consiste à tester si n divise 2 n 2 : dans le cas contraire, en vertu du petit théorème de Fermat, on conclut que n n est pas premier. Cependant il existe… …   Wikipédia en Français

  • Nombres de Poulet — Nombre et supernombre de Poulet Un test de primalité courant pour un nombre impair n consiste à tester si n divise 2 n 2 : dans le cas contraire, en vertu du petit théorème de Fermat, on conclut que n n est pas premier. Cependant il existe… …   Wikipédia en Français

  • Nombre de Poulet — Nombre et supernombre de Poulet Un test de primalité courant pour un nombre impair n consiste à tester si n divise 2 n 2 : dans le cas contraire, en vertu du petit théorème de Fermat, on conclut que n n est pas premier. Cependant il existe… …   Wikipédia en Français

  • Nombre et supernombre de Poulet — Un test de primalité courant pour un nombre impair n consiste à tester si n divise 2 n 2 : dans le cas contraire, en vertu du petit théorème de Fermat, on conclut que n n est pas premier. Cependant il existe des nombres composés qui passent… …   Wikipédia en Français

  • Supernombre de Poulet — Nombre et supernombre de Poulet Un test de primalité courant pour un nombre impair n consiste à tester si n divise 2 n 2 : dans le cas contraire, en vertu du petit théorème de Fermat, on conclut que n n est pas premier. Cependant il existe… …   Wikipédia en Français

  • Liste Des Matières De La Théorie Des Nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

  • Liste des matieres de la theorie des nombres — Liste des matières de la théorie des nombres Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

  • Liste des matières de la théorie des nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 Test de primalité e …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”