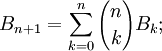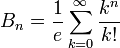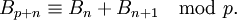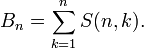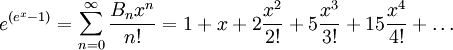Nombre de bell

Nombre de bell

Nombre de Bell

Page d'aide sur l'homonymie Pour les articles homonymes, voir Bell.

En mathématiques, les nombres de Bell, qui portent le nom de Eric Temple Bell, se rencontrent souvent en combinatoire. Ces nombres forment une suite d'entiers qui commence ainsi :

B_0=1,\quad B_1=1,\quad B_2=2,\quad B_3=5,\quad B_4=15,\quad B_5=52,\quad B_6=203,\quad\dots

(suite A000110 dans l'encyclopédie électronique des suites entières)

En général, Bn est le nombre de partitions d'un ensemble de cardinal n. (B0 est égal à 1 parce qu'il y a exactement une partition de l'ensemble vide. Une partition d'un ensemble E est par définition un ensemble de parties non vides et disjointes deux à deux, dont la réunion est égale à l'ensemble E.) Il en résulte que la seule partition de l'ensemble vide est... l'ensemble vide !

Les nombres de Bell satisfont la formule de récurrence :

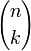B_{n+1}=\sum_{k=0}^{n}{n \choose k} B_k;

où {n \choose k} est un coefficient binomial.

Ils satisfont aussi à la formule de Dobinski :

B_n=\frac{1}{e}\sum_{k=0}^\infty \frac{k^n}{k!}

qui est le moment d'ordre n d'une loi de Poisson de paramètre 1.

Ils satisfont également à la congruence de Touchard : si p est un nombre premier quelconque alors

B_{p+n}\equiv B_n+B_{n+1}\mod p.

C'est une relation de congruence modulo p.

Chaque nombre de Bell est une somme des nombres de Stirling de deuxième espèce

B_n=\sum_{k=1}^n S (n, k).

La série génératrice exponentielle des nombres de Bell est

e^{(e^x-1)}=\sum_{n=0}^\infty \frac{B_nx^n}{n!}=1+x+2 \frac{x^2}{2!}+5 \frac{x^3}{3!} + 15 \frac{x^4}{4!} + \dots
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre de Bell ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre de bell de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Nombre De Bell — Pour les articles homonymes, voir Bell. En mathématiques, les nombres de Bell, qui portent le nom de Eric Temple Bell, se rencontrent souvent en combinatoire. Ces nombres forment une suite d entiers qui commence ainsi : (suite …   Wikipédia en Français

  • Nombre de Bell — Pour les articles homonymes, voir Bell. En mathématiques, le n ième nombre de Bell, qui porte le nom de Eric Temple Bell, est le nombre de partitions d un ensemble à n éléments ou, ce qui revient au même, le nombre de relations d équivalence sur… …   Wikipédia en Français

  • Bell — Saltar a navegación, búsqueda El termino Bell puede referirse a: El apellido de las siguientes personas: Alexander Graham Bell, científico, inventor y logopeda escocés y estadounidense John S. Bell, fisico norirlandes Charlie Bell, empresario… …   Wikipedia Español

  • Nombre De Stirling — En mathématiques, les nombres de Stirling apparaissent dans plusieurs problèmes combinatoires. Ils tirent leur nom de James Stirling, qui les a introduits au XVIIIe siècle. Il en existe deux sortes, nommés les nombres de Stirling de première …   Wikipédia en Français

  • Nombre de stirling — En mathématiques, les nombres de Stirling apparaissent dans plusieurs problèmes combinatoires. Ils tirent leur nom de James Stirling, qui les a introduits au XVIIIe siècle. Il en existe deux sortes, nommés les nombres de Stirling de première …   Wikipédia en Français

  • Bell 204/205 — Bell 204 / 205 Bell 205 del Departamento Contraincendios de Kern Country, California. Tipo Helicóptero utilitario Fabricante …   Wikipedia Español

  • Nombre de Stirling — En mathématiques, les nombres de Stirling apparaissent dans plusieurs problèmes combinatoires. Ils tirent leur nom de James Stirling, qui les a introduits au XVIIIe siècle. Il en existe deux sortes, nommés les nombres de Stirling de première …   Wikipédia en Français

  • Nombre de Catalan — En mathématiques combinatoires, les nombres de Catalan forment une suite de nombres naturels utilisée dans divers problèmes de dénombrement , impliquant souvent de façon récursive des objets définis. Ils sont nommés ainsi d après le mathématicien …   Wikipédia en Français

  • Nombre De Catalan — Nombres de Catalan Les nombres de Catalan sont des entiers naturels qui se rencontrent souvent dans les problèmes de combinatoire. Ils forment une suite dont le terme d indice n, appelé nème nombre de Catalan est défini par (voir coefficient… …   Wikipédia en Français

  • Nombre de Segner — Nombres de Catalan Les nombres de Catalan sont des entiers naturels qui se rencontrent souvent dans les problèmes de combinatoire. Ils forment une suite dont le terme d indice n, appelé nème nombre de Catalan est défini par (voir coefficient… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”