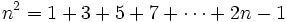Nombre Gnomonique

Parmi les nombres figurés, le nombre gnomonique est initialement le nombre qui dessine un gnomon. Le gnomon en grec signifie équerre, on le retrouve dans les cadrans solaires et en géométrie comme différence de deux rectangles. C'est ainsi que les premiers nombres gnomoniques sont issus de la différence de deux carrés.

Plus généralement, le gnomon est le morceau qui doit être ajouté à un graphique représentant un nombre figuré pour le transformer en le graphique représentant le nombre figuré de même type au rang suivant. Le nombre de points constituant le gnomon est alors appelé nombre gnomonique.

Exemples

Dans un triangle

Les nombres gnomoniques des nombres triangulaires sont les nombres linéaires 2, 3, 4, etc. car, pour passer du nombre triangulaire de rang n au nombre triangulaire de rang ""n + 1"" il suffit d'ajouter un gnomon constitué d'un segment de n + 1 points.

Dans un carré

Le gnomon d'un nombre carré ressemble à un ┌. Le carré de 8×8 éléments composé de gnomons peut être dessiné de la manière suivante:

8 8 8 8 8 8 8 8
8 7 7 7 7 7 7 7
8 7 6 6 6 6 6 6
8 7 6 5 5 5 5 5
8 7 6 5 4 4 4 4
8 7 6 5 4 3 3 3
8 7 6 5 4 3 2 2
8 7 6 5 4 3 2 1

Les nombres gnomiques carrés de rang 1, 2, 3, 4, 5, 6, 7, 8 sont donc les nombres impairs 1, 3, 5, 7, 9, 11, 13, 15.

Pour transformer un carré de n× n éléments en un carré de (n+1)×(n+1) éléments, on adjoint 2n + 1 éléments

• un à la fin de chaque rangée (n éléments),
• un à l'extrémité de chaque colonne (n éléments),
• et un seul dans le coin.

Par exemple, en transformant le carré de côté 7 en un carré de côté 8, on doit ajouter 15 éléments; ces ajouts sont les points de la figure ci-dessus portant l'étiquette 8.

On peut remarquer que cette technique gnomonique fournit également une vérification géométrique dans le cas particulier n=8, que la somme des n premiers nombres impairs est égale à n²; en effet la figure montre bien que 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = 64 = 8².

Les nombres gnomoniques des nombres carrés sont donc tous les nombres impairs. Le nombre gnomonique de rang n est 2n -1. Leur définition comme différence de deux carrés permet de procéder à des extraction de racine carrés et même de racine cubique

Nombre gnomonique et carré

Pour passer du nombre carré n² au nombre carré (n + 1)², il suffit d'ajouter le gnomon de rang n+1. On peut donc affirmer que

Cette propriété donne un moyen relativement simple de retrouver la racine d'un nombre carré: il suffit de lui ôter le nombre suffisant de nombres gnomoniques. Ainsi, 64 - 1 = 63; 63 - 3 = 60; 60 - 5 = 55; 55 - 7 = 48; 48 - 9 = 39; 39 - 11 = 28; 28 - 13 = 15; 15 - 15 = 0. Les soustractions des 8 premiers nombres impairs de 64 donnent 0; par conséquent, la racine carrée de 64 est égale à 8.

Le nombre de soustractions devenant très important à mesure que le nombre dont on extrait la racine grandit, il peut être réduit par une méthode semblable au procédé d'extraction de la racine enseigné à l'école. Par exemple 1225 = 35 ×35. Remarquons que la somme des chiffres de cette racine carrée: 3 + 5 = 8. Ce raccourci d'extraction de la racine ramène le nombre de soustractions de 35 à 8 soustractions seulement. Le raccourci utilise des astuces de marquage et de reprise. Cette méthode s'appelle la technique du goutte à goutte.

Nombre gnomonique et cube

Les cubes d'entiers naturels ou d'entiers strictement positifs peuvent être générés à partir de la suite S =(1, 3, 5, 7, ..., 2n + 1, ...) par des sommes mobiles, semblables aux moyennes mobiles en statistiques :

1. premier terme de S: 1 = 1³.
2. les deux termes suivants de S: 3 + 5 = 8 = 2³.
3. les trois termes suivants de S: 7 + 9 + 11 = 27 = 3³.
4. les quatre termes d'après de S: 13 + 15 + 17 + 19 = 64 = 4³.
5. les cinq termes suivants de S: 21 + 23 + 25 + 27 + 29 = 125 = 5³.
6. les six termes suivants de S: 31 + 33 + 35 + 37 + 39 + 41 = 216 = 6³.
7. les sept termes suivants de S: 43 + 45 + 47 + 49 + 51 + 53 + 55 = 343 = 7³.

Les « différences mobiles » de S donnent les racines cubiques.

• Portail des mathématiques