Approximation De Lubrification

Approximation De Lubrification: Approximation de lubrification

Lorsqu'un liquide est fortement confiné entre deux surfaces, c'est-à-dire que l'épaisseur de liquide est très faible devant les dimensions transversales des parois confinantes, il est possible de simplifier fortement l'équation de Navier-Stokes qui gouverne son écoulement : c'est l'approximation de lubrification, qui permet en particulier de décrire l'écoulement du liquide dans les contacts lubrifiés.

En effet, si 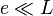$e \ll L$ (où $e$ est l'épaisseur moyenne entre les parois, et $L$ est la dimension transversale caractéristique des parois), alors :

la composante de la vitesse parallèle aux parois est très grande devant la composante perpendiculaire, que l'on peut négliger ;

la vitesse varie essentiellement dans la direction perpendiculaire aux parois : on peut donc négliger les dérivées de la vitesse par rapport aux coordonnées parallèles aux parois devant les dérivées par rapport à la coordonnée perpendiculaire ;

on peut considérer que la pression est constante dans la direction perpendiculaire aux parois.

Un aspect essentiel de cette approximation est que l'on peut négliger le terme inertiel -retrouvant ainsi l'équation de Stokes- lorsque 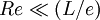$Re \ll (L/e)$ (où $R e$ est le nombre de Reynolds associé à l'écoulement), condition beaucoup moins restrictive que la condition habituelle 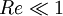$Re \ll 1$ dès lors que $L$ est très grand devant $e$ .

Demonstration

On rappelle l'équation de Navier-Stokes pour un fluide newtonien incompressible (bonne approximation pour les liquides) :
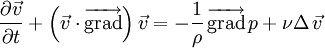$\frac{ \partial \vec{v} }{ \partial t } + \left(\vec{v} \cdot \overrightarrow{\mathrm{grad}}\right)\vec{v} = - \frac{1}{\rho}\,\overrightarrow{\mathrm{grad}}\,p + \nu \Delta\,\vec{v}$ ,
où : 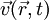$\vec{v} (\vec{r},t)$ est la vitesse du fluide ; 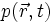$p (\vec{r},t)$ est la pression dans le fluide ; $ρ$ est la masse volumique du fluide ; $ν$ est la viscosité cinématique du fluide ; $t$ représente le temps ; 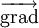$\overrightarrow{\mathrm{grad}}$ et $Δ$ sont respectivement les opérateurs différentiels gradient et laplacien.

Dans le cas d'un écoulement laminaire parfaitement parallèle (par exemple dans une conduite cylindrique), le terme inertiel présent dans l'équation de Navier-Stokes est rigoureusement nul :
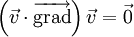$\left(\vec{v} \cdot \overrightarrow{\mathrm{grad}}\right)\vec{v} = \vec{0}$ .
Dans le cas d'un écoulement permanent, c'est-à-dire invariant dans le temps, la dérivée temporelle de la vitesse s'annule et on retrouve alors l'équation de Stokes, et ce quelle que soit la valeur du nombre de Reynolds. Lorsque les parois et donc l'écoulement ne sont pas tout à fait parallèles, dans quelle mesure est-il possible de négliger tout de même le terme inertiel ?

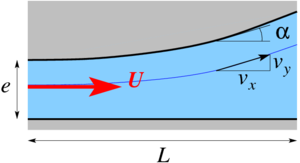
Schéma d'un écoulement fortement confiné

Considérons un liquide fortement confiné entre deux parois, comme représenté sur la figure ci-contre. Afin de simplifier cette étude, on se restreint à un écoulement à deux dimensions (le résultat reste valable pour un écoulement à trois dimensions). On peut projeter l'équation de Navier-Stokes sur les axes $O x$ et $O y$ :
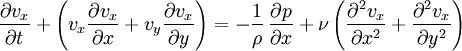
$\frac{ \partial v_x }{ \partial t } + \left( v_x \frac{ \partial v_x }{ \partial x } + v_y \frac{ \partial v_x }{ \partial y } \right) = - \frac{1}{\rho}\,\frac{ \partial p }{ \partial x } + \nu \left( \frac{ \partial^2 v_x }{ \partial x^2 } + \frac{ \partial^2 v_x }{ \partial y^2 } \right)$
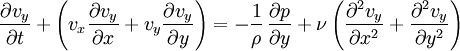
$\frac{ \partial v_y }{ \partial t } + \left( v_x \frac{ \partial v_y }{ \partial x } + v_y \frac{ \partial v_y }{ \partial y } \right) = - \frac{1}{\rho}\,\frac{ \partial p }{ \partial y } + \nu \left( \frac{ \partial^2 v_y }{ \partial x^2 } + \frac{ \partial^2 v_y }{ \partial y^2 } \right)$
On note $e$ l'épaisseur moyenne entre les parois, et $L$ l'échelle de variation typique de l'épaisseur (par exemple : taille du contact lubrifié ou période caractéristique de la rugosité des surfaces). On suppose que $e$ est très petit devant $L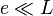$ : $e \ll L$ . D'autre part, on note $α$ l'angle formé par les deux surfaces confinant le liquide. Pour un angle petit, on peut écrire :
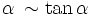$\alpha\,\sim \tan \alpha$ .
En remarquant que les variations de l'épaisseur sont inférieures ou de l'ordre de l'épaisseur elle-même, il vient finalement :
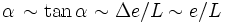$\alpha\,\sim \tan \alpha \sim \Delta e / L \sim e/L$ .
On peut alors estimer l'ordre de grandeur des termes présents dans l'équation de Navier Stokes. En notant $U$ la vitesse typique (vitesse moyenne) du liquide parallèlement aux parois et en remarquant que l'inclinaison des lignes de courant est de l'ordre de l'angle $α$ , on peut estimer l'ordre de grandeur des composantes de la vitesse :

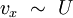$v_x\ \sim\ U$ ;

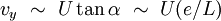$v_y\ \sim\ U \tan \alpha\ \sim\ U(e/L)$ .

Si l'épaisseur $e$ est très petite devant la longueur $L$ , on pourra donc négliger $v y$ devant $v x$ . Ainsi, dans l'équation de Navier-Stokes, les termes faisant intervenir $v y$ seront négligeables devant ceux faisant intervenir $v x$ . La projection sur O $y$ de l'équation de Navier-Stokes se simplifie alors fortement :
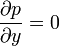$\frac{ \partial p }{ \partial y } = 0$ ,
indiquant que la variation de pression dans la direction perpendiculaire aux parois peut être négligée.

D'autre part l'échelle de variation de la vitesse perpendiculairement aux parois sera imposée par l'épaisseur $e$ entre celles-ci. La dérivée de la vitesse par rapport à $y$ sera donc de l'ordre de la valeur typique de la vitesse sur la longueur de variation typique, soit :
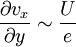$\frac{\partial v_x}{\partial y} \sim \frac{U}{e}$ .
De même, l'échelle de variation de la vitesse parallèlement aux parois sera $L$ et :
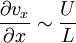$\frac{\partial v_x}{\partial x} \sim \frac{U}{L}$ .
En suivant la même démarche, on peut estimer les dérivées secondes de la vitesse selon $y$ :
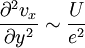$\frac{\partial^2 v_x}{\partial y^2} \sim \frac{U}{e^2}$ ;
et selon $x$ :
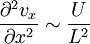$\frac{\partial^2 v_x}{\partial x^2} \sim \frac{U}{L^2}$ .
A partir de ces estimations, il est possible de comparer les amplitudes des différents termes intervenants dans l'équation de Navier-Stokes. On remarque tout d'abord que dans le terme visqueux, la dérivée seconde de la vitesse par rapport à $x$ , de l'ordre de $U / L 2$ , sera négligeable devant la dérivée seconde par rapport à $y$ , de l'ordre de $U / e 2$ , lorsque $e$ est très petit devant $L$ . Le terme visqueux se réduit alors à :
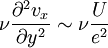$\nu \frac{ \partial^2 v_x }{ \partial y^2 } \sim \nu \frac{U}{e^2}$ .
Les deux composantes du terme inertiel seront par contre du même ordre de grandeur :

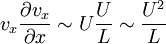$v_x \frac{\partial v_x}{\partial x} \sim U \frac{U}{L} \sim \frac{U^2}{L}$ ;

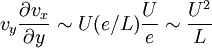$v_y \frac{\partial v_x}{\partial y} \sim U(e/L) \frac{U}{e} \sim \frac{U^2}{L}$ .

Le terme inertiel sera donc négligeable devant le terme visqueux lorsque :
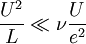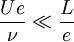$\frac{U^2}{L} \ll \nu \frac{U}{e^2}$ , soit : $\frac{Ue}{\nu} \ll \frac{L}{e}$ .
On reconnait dans le premier membre le nombre de Reynolds associé à l'écoulement. La condition de validité de l'approximation de lubrification s'écrit donc :
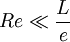$Re \ll \frac{L}{e}$ , avec $e \ll L$ .
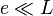En régime permanent, l'écoulement du liquide est finalement gouverné par le jeu d'équations suivant :

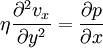$\eta \frac{\partial^2 v_x}{\partial y^2} = \frac{\partial p}{\partial x}$ ;

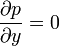$\frac{\partial p}{\partial y} = 0$ ;

Bibliographie

(en) G.K. Batchelor, An Introduction to Fluid Dynamics [« Introduction à la dynamique des fluides »], Cambridge University Press, 1967.

(fr)E. Guyon, J.-P. Hulin, L. Petit, Hydrodynamique physique, CNRS Editions - EDP Sciences, 2^e éd. (1^re éd. 1991), 2001.

Ce document provient de « Approximation de lubrification ».

Catégorie : Mécanique des fluides

Contenu soumis à la licence CC-BY-SA. Source : Article Approximation De Lubrification de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Approximation de lubrification — Mince couche de liquide mélangée à des particules, coulant le long d un plan incliné. Lorsqu un liquide est fortement confiné entre deux surfaces, c est à dire que l épaisseur de liquide est très faible devant les dimensions transversales des… … Wikipédia en Français
Ecoulement de Poiseuille — Écoulement de Poiseuille La loi de Poiseuille (également appelée loi de Hagen Poiseuille) est nommée à partir des travaux de Jean Louis Marie Poiseuille, médecin et physicien français du XIXe siècle[1]. Un écoulement de Poiseuille est un… … Wikipédia en Français
Loi de Poiseuille — Écoulement de Poiseuille La loi de Poiseuille (également appelée loi de Hagen Poiseuille) est nommée à partir des travaux de Jean Louis Marie Poiseuille, médecin et physicien français du XIXe siècle[1]. Un écoulement de Poiseuille est un… … Wikipédia en Français
Écoulement de Poiseuille — La loi de Poiseuille (également appelée loi de Hagen Poiseuille) décrit l écoulement laminaire (c est à dire à filets d’eau parallèles) d un liquide visqueux dans une conduite cylindrique. Découverte indépendamment en 1844 par le médecin et… … Wikipédia en Français
Écoulement de poiseuille — La loi de Poiseuille (également appelée loi de Hagen Poiseuille) est nommée à partir des travaux de Jean Louis Marie Poiseuille, médecin et physicien français du XIXe siècle[1]. Un écoulement de Poiseuille est un écoulement qui suit une loi de… … Wikipédia en Français
Force Normale Entre Deux Disques Dans Un Fluide Visqueux — Soient deux disques parallèles et rigides, de rayon R, s approchant à la vitesse V au sein d un fluide visqueux incompressible, de viscosité η, dans le régime de Stokes (faibles nombres de Reynolds) Il s exerce entre eux, via le fluide, une force … Wikipédia en Français
Force normale entre deux disques dans un fluide visqueux — Les adhésifs sont très utilisés dans la vie courante et dans l industrie. La raison pour laquelle ils résistent à la séparation provient d une part de leur minceur qui est l ingrédient principal de leur résistance initiale au décollement, et d… … Wikipédia en Français
Calcul De Vis D'assemblage — Sur une vis d assemblage, du fait de la force générée lors du serrage, plusieurs sollicitations apparaissent dans le système vis écrou. La forme de la vis et le filetage apportent de plus, des concentrations de contraintes. Ainsi on doit prendre… … Wikipédia en Français
Calcul de vis d'assemblage — Sur une vis d assemblage, du fait de la force générée lors du serrage, plusieurs sollicitations apparaissent dans le système vis écrou. La forme de la vis et le filetage apportent de plus, des concentrations de contraintes. Ainsi on doit prendre… … Wikipédia en Français
SURFACE (PHÉNOMÈNES DE) — La surface d’un solide ou d’un liquide est une région s’étendant sur quelques distances atomiques qui sépare l’intérieur du matériau du milieu extérieur: en général, le vide ou un gaz. Si le milieu extérieur est une autre phase dense, liquide ou… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Approximation De Lubrification

Approximation de lubrification

Demonstration

Bibliographie

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Approximation De Lubrification

Approximation de lubrification

Demonstration

Bibliographie

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link