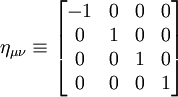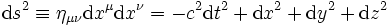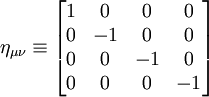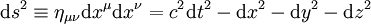Métrique minkowskienne
- Métrique minkowskienne
-
Métrique de Minkowski
En notant 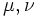 des indices d'espace-temps à 4 dimensions la métrique de Minkowski s'écrit, avec la signature ( − ; + ; + ; + ) :
des indices d'espace-temps à 4 dimensions la métrique de Minkowski s'écrit, avec la signature ( − ; + ; + ; + ) :
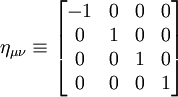
(cette matrice est en fait une matrice de symétrie par rapport à un hyperplan.)
ou bien sous forme différentielle
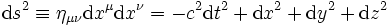
Une autre possibilité est de choisir la signature ( + ; − ; − ; − ) :
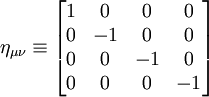
la forme différentielle est alors
 Portail de la physique
Portail de la physique
Catégorie : Relativité générale
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Métrique minkowskienne de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Tenseur metrique — Tenseur métrique Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel … Wikipédia en Français
Tenseur métrique — En géométrie et plus particulièrement en géométrie différentielle, le tenseur métrique est un tenseur d ordre 2 qui est utilisé pour la mesure des distances et des angles. Il généralise le théorème de Pythagore. Dans un système de coordonnées… … Wikipédia en Français
D'alembertien — Le d alembertien, ou opérateur d alembertien est la généralisation du concept du laplacien dans une métrique minkowskienne. Il apparaît en particulier en électromagnétisme pour décrire la propagation des ondes électromagnétiques ainsi que dans l… … Wikipédia en Français
Opérateur d'Alembertien — D alembertien Articles d analyse vectorielle Objets d ét … Wikipédia en Français
Opérateur d'alembertien — D alembertien Articles d analyse vectorielle Objets d ét … Wikipédia en Français
RELATIVITÉ — En physique, le vocable «relativité» recouvre deux concepts très différents. Celui de relativité restreinte (qui a remplacé la relativité galiléenne ) spécifie la structure cinématique de l’espace temps. Cette structure, d’abord suggérée par… … Encyclopédie Universelle
Espace De Minkowski — Un espace de Minkowski, du nom de son inventeur Hermann Minkowski, est un espace affine mathématique à quatre dimensions modélisant l espace temps de la relativité restreinte : les propriétés physiques présentes dans cette théorie d Einstein … Wikipédia en Français
Espace de Minkowski — Un espace de Minkowski, du nom de son inventeur Hermann Minkowski, est un espace affine mathématique à quatre dimensions modélisant l espace temps de la relativité restreinte : les propriétés physiques présentes dans cette théorie… … Wikipédia en Français
Espace de minkowski — Un espace de Minkowski, du nom de son inventeur Hermann Minkowski, est un espace affine mathématique à quatre dimensions modélisant l espace temps de la relativité restreinte : les propriétés physiques présentes dans cette théorie d Einstein … Wikipédia en Français
Ligne D'univers — En physique, la ligne d univers d un objet est la trajectoire d un objet lorsqu il voyage à travers l espace temps en 4 dimensions. Le concept de ligne d univers se distingue du concept de l « orbite » ou de la « trajectoire » … Wikipédia en Français
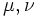 des indices d'espace-temps à 4 dimensions la métrique de Minkowski s'écrit, avec la signature ( − ; + ; + ; + ) :
des indices d'espace-temps à 4 dimensions la métrique de Minkowski s'écrit, avec la signature ( − ; + ; + ; + ) :