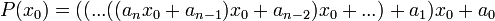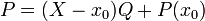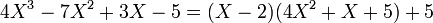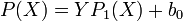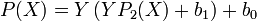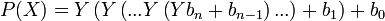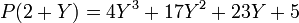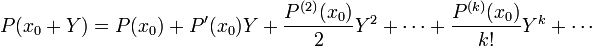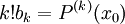Méthode De Horner

Méthode De Horner

Méthode de Ruffini-Horner

Connue sous le nom de méthode de Horner, règle de Ruffini ou algorithme de Ruffini-Horner, cette méthode se décline sur plusieurs niveaux. Elle permet de calculer la valeur d'un polynôme en 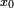\scriptstyle x_0. Elle présente un algorithme simple effectuant la division euclidienne d'un polynôme par 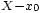\scriptstyle X - x_0. Mais elle offre aussi une méthode de changement de variable 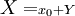X=\scriptstyle x_0 + Y dans un polynôme. C'est sous cette forme qu'elle est utilisée pour déterminer une valeur approchée d'une racine d'un polynôme.

Sommaire

Histoire

La méthode de Ruffini-Horner de recherche d'une valeur approchée de racine d'un polynôme est publiée à quelques années d'intervalle par Paolo Ruffini (1804-1807-1813) et par William George Horner (1819-1845 posthume) mais il semble bien que Horner n'ait pas eu connaissance des travaux de Ruffini. La méthode de Horner est ensuite popularisée par les mathématiciens De Morgan et J.R. Young. Dans leurs premières publications, ces deux auteurs utilisent des méthodes de dérivations pour effectuer le changement de variable X = x0 + Y. Par la suite, ils présentent des versions ne faisant appel qu'à des techniques algébriques. La méthode de Ruffini-Horner est difficilement exploitable si le polynôme possède deux racines trop proches. Ruffini n'évoque pas ce problème mais Horner propose une procédure spéciale pour ce cas-là[1].

En tant que technique de changement de variable, on retrouve des algorithmes analogues, en Chine, pour l'extraction de racine n-ième, dans les Neuf Chapitres (263 après J.C) [2]et dans l'œuvre de Al Samaw'al (XIIe siècle)[3]. Mais il semble bien que Sharaf al-Dīn al-Tūsī (XIIe siècle) soit le premier à l'utiliser dans le cas général d'une équation de degré 3 [4].

Valeur d'un polynôme en un point

Soit 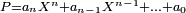\scriptstyle P =a_nX^n + a_{n-1}X^{n-1} + ... + a_0 un polynôme [5] et 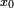\scriptstyle x_0 un nombre [6]. Le calcul de 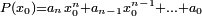\scriptstyle P(x_0) = a_nx_0^n + a_{n-1}x_0^{n-1} + ... + a_0 laisse à penser qu'il faut calculer chacune des puissances de 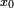\scriptstyle x_0, multiplier celle-ci par son coefficient ak puis faire la somme de ce que l'on a trouvé.

Si on calcule 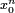\scriptstyle x_0^n en multipliant successivement 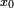\scriptstyle x_0 par lui-même, le nombre de produits nécessaire est alors de n + (n − 1) + ... + 2 + 1 = n(n + 1) / 2, quantité qui croît comme le carré du degré du polynôme.

On peut améliorer la vitesse du calcul de 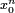\scriptstyle x_0^n par une méthode d'exponentiation rapide, permettant de réduire le temps du calcul de 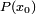\scriptstyle P(x_0) à une quantité qui croît comme nln(n).

La méthode de Horner consiste à améliorer encore ce résultat en effectuant le calcul comme suit :

P(x_0) = ((...((a_nx_0 + a_{n-1})x_0 + a_{n-2})x_0 + ... ) + a_1)x_0 + a_0\,

Le nombre de produits est alors réduit à n, de sorte que le temps de calcul d'une fonction polynomiale en un point a est seulement proportionnel au degré du polynôme. La méthode consiste donc à multiplier le premier coefficient par 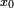\scriptstyle x_0 et à lui ajouter le second coefficient. On multiplie alors le nombre obtenu par 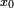\scriptstyle x_0 et on lui ajoute le troisième coefficient, etc. Elle s'organise très bien à l'aide d'un tableau dans lequel chaque case de la seconde ligne est obtenue en multipliant le coefficient de la case de gauche par 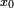\scriptstyle x_0 et en lui ajoutant le coefficient de la case du dessus.

Coefficients de P an an - 1 an - 2 ... a1 a0
Facteur x0 an anx0 + an - 1 (anx0 + an - 1)x0 + an-2 ... q0 P(x0)=q0x0 + a0

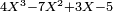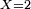
Exemple pratique : Calcul de \scriptstyle 4X^3 - 7X^2 + 3X - 5 pour \scriptstyle X=2

Coefficients de P 4 − 7 3 − 5
Facteur 2 4 8 − 7 = 1 2 + 3 = 5 P(2) = 10 − 5 = 5

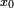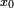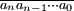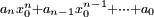Cette méthode permet aussi d'effectuer une conversion rapide d'un nombre écrit en base \scriptstyle x_0 en écriture en base 10. En effet, si un nombre s'écrit, en base \scriptstyle x_0, \scriptstyle \overline{a_na_{n-1}\cdots a_0}, ce nombre vaut \scriptstyle a_nx_0^n+a_{n-1}x_0^{n-1}+\cdots+ a_0.

Exemple pratique : écriture en base 10 du nombre hexadécimal DA78

Coefficients 13 10 7 8
Facteur 16 13 13 × 16 + 10 = 218 218 ×16+ 7 = 3495 DA78 = 3495 × 16 + 8 = 55928


Quotient d'un polynôme par X - x0

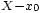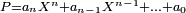Cette même méthode permet aussi d'obtenir la division d'un polynôme par \scriptstyle X-x_0. Soit \scriptstyle P = a_nX^n + a_{n-1}X^{n-1} + ... + a_0.

La division euclidienne de P par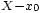\scriptstyle X-x_0 donne

P = (X-x_0)Q + P(x_0)\,

où Q est un polynôme de degré n - 1.

Si on écrit 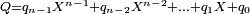\scriptstyle Q = q_{n-1}X^{n - 1} + q_{n-2}X^{n-2}+ ...+ q_1X + q_0 et si on identifie les coefficients de même degré dans les deux membres, on obtient :

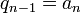
q_{n-1} = a_n \,
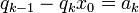q_{k-1} - q_kx_0=a_k \, pour tout k tel que 0 < k < n

Soit encore

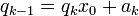q_{k-1}=q_kx_0+a_k\, pour tout k tel que 0 < k < n


Les n valeurs de la suite q calculées ici sont précisément les n valeurs successives calculées dans le paragraphe précédent pour évaluer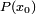\scriptstyle P(x_0). La mémorisation de ces valeurs successives donne donc les coefficients du polynôme quotient, la dernière valeur étant celle du reste.

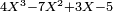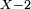
Application pratique : Division euclidienne de \scriptstyle 4X^3 - 7X^2 + 3X - 5 par \scriptstyle X-2

Il suffit de reprendre le tableau précédemment construit et de lire dans les cases de la seconde ligne les coefficients de Q.

Coefficients de P 4 − 7 3 − 5
Coeficients de Q 4 8 − 7 = 1 2 + 3 = 5 Reste = 10 − 5 = 5

Donc

4X^3 - 7X^2 + 3X - 5 = (X-2)(4X^2 + X + 5) + 5\,

Changement de variable

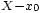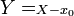L'algorithme précédent permet donc d'effectuer la division euclidienne du polynome P par \scriptstyle X-x_0. On peut alors écrire, en posant Y = \scriptstyle X-x_0.

P(X) = YP_1(X)+b_0\,

En utilisant de nouveau l'algorithme pour 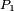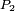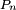\scriptstyle P_1, \scriptstyle P_2, .. \scriptstyle P_n,on obtient successivement

P(X) = Y\left(YP_2(X)+b_1\right)+b_0\,

...

P(X) = Y\left(Y\left(...Y\left(Yb_n + b_{n-1}\right)...\right)+b_1\right)+b_0\,

Les nombres 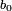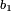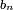\scriptstyle b_0, \scriptstyle b_1, ...\scriptstyle b_n sont donc les coefficients du polynôme Q tel que Q(Y) = P(x0+Y)


Illustration pratique  : Si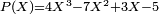 \scriptstyle P(X) =4X^3 - 7X^2 + 3X - 5 et que l'on cherche à écrire 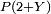\scriptstyle P(2 + Y) , on applique 4 fois la méthode de division euclidienne par X - 2 :

Coefficients de P 4 − 7 3 − 5
Coeficients de P1 4 8 − 7 = 1 2 + 3 = 5 10 − 5 = 5
Coeficients de P2 4 8 + 1 =9 18 + 5 = 23
Coeficients de P3 4 8 + 9 =17
Coeficients de P4 4

Donc

P(2 + Y) = 4Y^3+17Y^2+23Y+5\,

Valeur approchée d'une racine

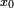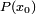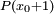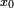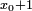Pour chercher la valeur approchée x d'une racine d'un polynôme P, on cherche un entier \scriptstyle x_0 tel que \scriptstyle P(x_0) et \scriptstyle P( x_0+1) soient de signe contraire. On sait alors, d'après le théorème des valeurs intermédiaires, qu'il existe une racine entre \scriptstyle x_0 et \scriptstyle x_0 + 1. On pose alors 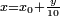\scriptstyle x = x_0 + \frac{y}{10}. Le nombre x est racine de P(X) si et seulement si le nombre y/10 est racine de 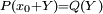\scriptstyle P(x_0+Y) = Q(Y). Ce polynôme Q se détermine grâce à la méthode de Horner. Enfin x est racine de P(X) si et seulement y est racine d'un polynôme R(X) obtenu en multipliant les coefficients bk de Q par 10n − k.

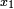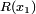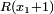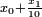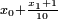Il s'agit alors de chercher une racine de R comprise entre 0 et 10 en utilisant un processus analogue : on cherche un entier \scriptstyle x_1 compris entre 0 et 9 tels que \scriptstyle R(x_1) et \scriptstyle R(x_1 + 1) soient de signe contraire. On sait alors qu'il existe une racine x de P comprise entre \scriptstyle x_0+\frac{x_1}{10} et \scriptstyle x_0+\frac{x_1+1}{10}...

On détermine ainsi les décimales successives du développement décimal de x.

Exemple : Algorithme de Ruffini-Horner pour l'extraction de la racine cubique de 18.

Il s'agit de trouver un réel x racine du polynôme 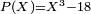\scriptstyle P(X) = X^3 - 18. On sait immédiatement que P(2)< 0 et P(3) > 0, x est donc compris entre 2 et 3. On pose alors 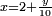\scriptstyle x=2+\frac{y}{10} et on cherche le polynôme Q tel que P(2+Y)=Q(Y)

Coefficients de P 1 0 0 - 18
Coeficients de P1 1 2 4 - 10
Coeficients de P2 1 4 12
Coeficients de P3 1 6
Coeficients de P4 1

Le réel x est racine cubique de 18 si 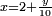\scriptstyle x=2+\frac{y}{10} où y est racine de 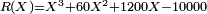\scriptstyle R(X)= X^3+60X^2+1200X-10000. La racine y est comprise entre 6 et 7 (pour éviter de balayer tous les nombres, il suffit de remarquer que 1200y et 10000 doivent être très proches avec 1200y < 10000 ). On pose alors 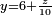\scriptstyle y=6+\frac{z}{10} et on cherche le polynôme S tel que R(6+Z)=S(Z).

Coefficients de R 1 60 1200 -10000
Coeficients de R1 1 66 1596 -424
Coeficients de R2 1 72 2028
Coeficients de R3 1 78
Coeficients de R4 1

Le réel y est racine de R si 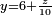\scriptstyle y=6+\frac{z}{10} où z est racine de 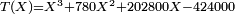\scriptstyle T(X)= X^3+780X^2+202800X-424000. La racine z est comprise entre 2 et 3. Donc y est compris entre 6,2 et 6,3 et x est compris entre 2,62 et 2,63.

Dérivées successives de P en x0

Cette propriété apparaît ici en dernière position alors qu'elle est la propriété initiale mise en évidence par Ruffini et Horner. Cependant, comme une démarche purement algébrique est possible, celle-ci, plus simple, a été présentée d'abord. Le même algorithme permet de déterminer aussi la valeur de 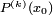\scriptstyle P^{(k)}(x_0). En effet, le développement de Taylor de P(x0 + Y) donne

P(x_0+Y) = P(x_0) + P'(x_0)Y + \frac{P^{(2)}(x_0)}{2}Y^2+\cdots+\frac{P^{(k)}(x_0)}{k!}Y^k + \cdots \,

Si on note Q(Y) = P(a + Y), les coefficients bk de Q, trouvés par la méthode de Ruffini-Horner vérifient l'égalité

k!b_k=P^{(k)}(x_0)\,


Annexes

Notes et références

  1. ↑ Florian Cajori Horner's method of approximation anticipated by Ruffini, American Mathematical Society, 21 novembre 1910.
  2. ↑ Karine Chemla, Guo Shuchun, Neuf Chapitres. Le Classique de la Chine ancienne et ses commentaires. Edition critique" [détail des éditions], introduction au chapitre 4
  3. ↑ Hélène Bellosta, À propos de l'histoire des sciences arabes, Gazette des mathématiciens, n°82, Octobre 1999
  4. ↑ J. L. Berggren (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", Journal of the American Oriental Society 110 (2), p. 304-309.
  5. ↑ On peut travailler sur R ou sur un anneau commutatif A quelconque
  6. ↑ ou un élément de l'anneau A
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « M%C3%A9thode de Ruffini-Horner ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Méthode De Horner de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Methode de Horner — Méthode de Ruffini Horner Connue sous le nom de méthode de Horner, règle de Ruffini ou algorithme de Ruffini Horner, cette méthode se décline sur plusieurs niveaux. Elle permet de calculer la valeur d un polynôme en . Elle présente un algorithme… …   Wikipédia en Français

  • Méthode d'Horner — Méthode de Ruffini Horner Connue sous le nom de méthode de Horner, règle de Ruffini ou algorithme de Ruffini Horner, cette méthode se décline sur plusieurs niveaux. Elle permet de calculer la valeur d un polynôme en . Elle présente un algorithme… …   Wikipédia en Français

  • Méthode de Horner — Méthode de Ruffini Horner Connue sous le nom de méthode de Horner, règle de Ruffini ou algorithme de Ruffini Horner, cette méthode se décline sur plusieurs niveaux. Elle permet de calculer la valeur d un polynôme en . Elle présente un algorithme… …   Wikipédia en Français

  • Méthode de Hörner — Méthode de Ruffini Horner Connue sous le nom de méthode de Horner, règle de Ruffini ou algorithme de Ruffini Horner, cette méthode se décline sur plusieurs niveaux. Elle permet de calculer la valeur d un polynôme en . Elle présente un algorithme… …   Wikipédia en Français

  • Méthode de horner — Méthode de Ruffini Horner Connue sous le nom de méthode de Horner, règle de Ruffini ou algorithme de Ruffini Horner, cette méthode se décline sur plusieurs niveaux. Elle permet de calculer la valeur d un polynôme en . Elle présente un algorithme… …   Wikipédia en Français

  • Méthode de Ruffini-Horner — En mathématiques et algorithmique, la méthode de Horner, connue aussi sous les noms de règle de Ruffini ou algorithme de Ruffini Horner, se décline sur plusieurs niveaux. Elle permet de calculer la valeur d un polynôme en . Elle présente un… …   Wikipédia en Français

  • Horner — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Horner est un nom de famille anglais qui dérive de l occupation de l écorneur (horner), une personne qui coupe les cornes (horns) du bétail, ou qui fait… …   Wikipédia en Français

  • Méthode de résolution numérique — Analyse numérique Simulation numérique d un crash de véhicule L’analyse numérique est une discipline des mathématiques. Elle s’intéresse tant aux fondements théoriques qu’à la mise en pratique des méthodes permettant de résoudre, par des calculs… …   Wikipédia en Français

  • Méthode numérique — Analyse numérique Simulation numérique d un crash de véhicule L’analyse numérique est une discipline des mathématiques. Elle s’intéresse tant aux fondements théoriques qu’à la mise en pratique des méthodes permettant de résoudre, par des calculs… …   Wikipédia en Français

  • Schéma de Horner — Méthode de Ruffini Horner Connue sous le nom de méthode de Horner, règle de Ruffini ou algorithme de Ruffini Horner, cette méthode se décline sur plusieurs niveaux. Elle permet de calculer la valeur d un polynôme en . Elle présente un algorithme… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”