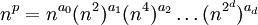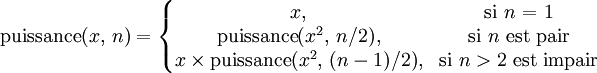Exponentiation Rapide

L'exponentiation rapide est un algorithme utilisé pour calculer rapidement, de grandes puissances entières. En anglais, cette méthode est aussi appelée square-and-multiply (« mettre au carré et multiplier »).

Sommaire 1 Écriture mathématique 2 Algorithme 3 Exemples d'implémentation 4 Voir aussi

Écriture mathématique

La première façon de calculer une puissance n^p, est de multiplier n par lui-même p fois. Cependant, il existe des méthodes bien plus efficaces, où le nombre d'opérations nécessaires n'est plus de l'ordre de p mais de l'ordre de log(p), pour le logarithme en base 2. On peut par exemple écrire 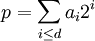pour 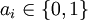, et on constate alors que :

Il faut ainsi d opérations pour calculer tous les 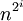, puis d opérations supplémentaires pour former le produit des 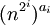pour i variant. Le nombre d'opérations total est donc 2d, qui est bien de l'ordre du logarithme de p. Cette simple remarque algébrique conduit par exemple à l'algorithme ci-dessous.

Algorithme

Soit n un entier strictement supérieur à 1, supposons que l'on sache calculer pour tout x appartenant à l'ensemble des réels, toutes les puissances x^k de x, pour tout k, tel que .

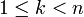• Si n est pair alors xⁿ = (x²)^{n / 2}. Il suffit alors de calculer y^{n / 2} avec y = x².
• Si n est impair et n>1, alors 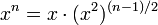. Il suffit de calculer y^{(n − 1) / 2} avec y = x² et de multiplier par x le résultat.

Cette remarque nous amène à l'algorithme récursif suivant qui calcule xⁿ pour un entier strictement positif n:

En comparant à la méthode ordinaire qui consiste à multiplier x par lui-même n-1 fois, cet algorithme nécessite de l'ordre de O(lg n) multiplications et ainsi accélère le calcul de xⁿ de façon spectaculaire pour les grands entiers.

La méthode fonctionne dans tout semi-groupe et est souvent utilisée pour calculer des puissances de matrices, et particulièrement en cryptographie, mais aussi pour calculer les puissances dans un anneau d'entiers modulo q. Elle peut être aussi utilisée pour calculer des puissances d'un élément dans un groupe, en utilisant pour les puissances négatives la règle : puissance(x, -n) = (puissance(x, n))^-1.

Exemples d'implémentation

Voici une implémentation itérative de l'algorithme précédent, dans le langage de programmation Ruby. Dans la plupart des langages, vous aurez besoin de remplacer resultat=1 par resultat=matrice_unite_de_la_meme_taille_que_x, pour obtenir le programme de calcul d'une puissance d'une matrice. En Ruby, resultat s'adapte automatiquement au type approprié. Ainsi, cette fonction s'utilise aussi bien avec les matrices, qu'avec les entiers ou les réels.

def puissance(x,n)
    resultat = 1
    while (n != 0)
        # si n est impair, on multiplie resultat par x
        if ((n % 2) == 1) then
            resultat = resultat * x
            n=n-1
        end
        x = x*x
        n = n/2
    end
    return resultat
end

Un autre exemple d'implémentation, cette fois en Pascal, et en utilisant la récursivité.

function puissance(x,n:longint):longint;
var intermediaire:longint;
begin
	if n=1 then
		puissance:=x
	else
		begin
			intermediaire:=puissance(x,n div 2);
			if (n mod 2)=0 then
				puissance:=intermediaire*intermediaire
			else
				puissance:=intermediaire*intermediaire*x;
		end
end;

Enfin, un exemple dans un langage fonctionnel, OCaml. Pour travailler en toute généricité, on fournit à la fonction une fonction de multiplication (correspondant au * sur les entiers) et un élément neutre (correspondant à 1). Cela permet par exemple de faire une exponentiation rapide sur les polynômes.

let rec puissance neutre ( * ) a = function
  0 -> neutre
| n -> let b = puissance neutre ( * ) (a * a) (n / 2) in
       if n mod 2 = 0 then b else a * b;;

On peut aussi observer que cette fonction permet de faire une multiplication rapide en ne se servant que de la fonction d'addition : "puissance 0 ( + ) 3 7" renvoie bien 21.

Voir aussi

• Suite de Fibonacci
• Exponentiation modulaire

• Portail des mathématiques