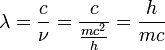- Mécanique Ondulatoire
-
Mécanique ondulatoire
La mécanique ondulatoire est la forme initiale de la mécanique quantique avant que celle-ci ne soit formalisée au début des années 1920 par Niels Bohr, Erwin Schrödinger et Wolfgang Pauli. La mécanique ondulatoire considérait les particules comme des ondes réelles matérielles, comme semblait l'indiquer la dualité onde-corpuscule mise en évidence par Louis de Broglie. La mécanique quantique a abandonné cette vision des choses en faveur d'ondes immatérielles de probabilité.
Sommaire
Origines
L'origine de la mécanique ondulatoire se situe au début du XXe siècle ; elle commence avec les travaux d'Albert Einstein qui associe un quantum d'énergie à l'onde électromagnétique, à la suite des travaux de Max Planck sur le corps noir. Elle se complète avec Louis de Broglie qui définit le comportement des électrons sous forme d'onde.
De ces antagonismes est né ce que l'on appelle la "dualité onde-particule".
Histoire de la mécanique ondulatoire
Louis de Broglie eut l'idée d'associer une fonction d'onde à chaque particule : cela implique que l'espace n'est pas uniquement constitué de particules, mais de champs quantiques qui engendrent des forces entre les corps. Par la suite, Albert Einstein et Erwin Schrödinger s'intéressèrent aux travaux de De Broglie : Erwin Schrödinger remplaça tous les niveaux d'énergie par des configurations ondulatoires et publia sa fameuse équation en 1926.
Mais la théorie se heurtait à certaines observations concernant les paquets d'ondes. Ce fut Max Born qui trouva la solution du problème par les probabilités. Une nouvelle idée est instaurée : les atomes ne sont plus traités individuellement, mais de manière statistique.
Ainsi l'ensemble de ces travaux renseigne sur la probabilité statistique de l'énergie d'un système.
Définition mathématique
À toute particule de masse m et de vitesse v était associée une onde de longueur d'onde λ, de fréquence ν et de quantité de mouvement p = mv.
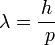
Si nous représentons la trajectoire d'un électron par une corde de violon en vibration, l'analyse de Fourier démontre que les sons se forment à partir d'un nombre entier d'ondes fondamentales.
La fonction d'onde décrit les états propres de quantité de mouvement. Plus la fonction d'onde est resserrée, plus la fréquence est élevée.
Une particule est une onde qui se propage dans tout l'espace dont l'amplitude de probabilité nous permet de connaître la position à un moment t.
Démonstration mathématique
Dans sa thèse[1] (p 33 et suivantes, numérotation en haut de page), de Broglie utilise les hypothèses suivantes :
1) "Relation du quantum"
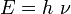 : entraîne l'existence d'une périodicité, sans qu'on puisse encore présumer quoi au juste est ainsi pulsatoire ou cyclique.
: entraîne l'existence d'une périodicité, sans qu'on puisse encore présumer quoi au juste est ainsi pulsatoire ou cyclique.2) "Harmonie des phases" : donne la relation de dispersion vvφ = c2 grâce à la transformation de Lorentz.
3) Relation d'Einstein E = mc2 : combinée à celle du quantum et de l'harmonie des phases, donne la longueur d'onde, rapport de la vitesse de phase à la fréquence.
Hypothèse de conservation de la phase
La "relation du quantum"
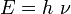 implique l'existence d'une fréquence interne ν associée à chaque particule, matérielle ou non, que ce soit un électron ou un photon. Ensuite, de Broglie fait l'hypothèse dite de "l'harmonie des phases" (thèse, p 35), où le "phénomène périodique" de fréquence ν’ dans le référentiel propre R’ de la particule est "constamment en phase avec une onde se propageant dans la même direction que le mobile".
implique l'existence d'une fréquence interne ν associée à chaque particule, matérielle ou non, que ce soit un électron ou un photon. Ensuite, de Broglie fait l'hypothèse dite de "l'harmonie des phases" (thèse, p 35), où le "phénomène périodique" de fréquence ν’ dans le référentiel propre R’ de la particule est "constamment en phase avec une onde se propageant dans la même direction que le mobile".L’amplitude ce phénomène périodique est, à un coefficient près, représentée par une "fonction sinusoïdale" avec une phase nulle au départ :
- sin(2πν't')
Dans le référentiel R du laboratoire, v est la vitesse de la particule, x son abscisse et t le temps de l’observateur, mesuré par une horloge du laboratoire. Appliquons la transformation de Lorentz du temps pour obtenir le temps propre t' à partir du temps t du laboratoire :
En remplaçant t’ par cette expression, l’amplitude de l’onde s’écrit, en utilisant le temps t de l’observateur
Or, selon la définition de la phase, l’amplitude d’une onde de vitesse de phase vφ s’écrit :
Les deux expressions précédentes représentent le même phénomène dans le référentiel R’, on a en les identifiant[2] :
où β = v / c
La vitesse c de la lumière est donc la moyenne géométrique des vitesses v de la particule et de phase vφ de l’onde associée. Comme la vitesse v de la particule ne peut dépasser la vitesse c de la lumière, la vitesse de phase vφ lui est toujours supérieure. Elle est infinie pour une particule de vitesse nulle, en accord avec Newton pour qui la transmission des forces était instantanée. Ce n’est pas contradictoire avec la relativité non plus puisque la vitesse de phase correspond à la vitesse de transmission des zéros de l’onde où, l’amplitude étant nulle, il n’y a pas transmission d’énergie. La vitesse de groupe étant celle du plus grand des maximums, la distance entre deux maximums successifs est variable et peu précise. On doit donc définir la longueur d’onde dans un paquet d’ondes par la distance entre deux noeuds consécutifs et non entre deux maximums alors que c'est sans importance pour une onde plane et sinusoïdale.
Une vitesse de phase supérieure à celle de la lumière est bien connue dans les guides d’ondes. Une vague venue du large, perpendiculaire à la digue, déferle instantanément le long de la digue ou à une vitesse supérieure à sa vitesse propre. Un phénomène du même genre, observé dans le Cosmos, a pu faire croire à l’existence de vitesses « superluminales » dans des quasars et pulsars.
L’identification des mêmes formules donne aussi la fréquence ν dans le référentiel R de l’observateur :
La variation de fréquence est négligeable aux vitesses faibles par rapport à celle de la lumière. Par contre la variation de phase ne l'est pas, même pour v << c.
Longueur d'onde de de Broglie
Dans sa thèse, Louis de Broglie écrit :
« On peut donc concevoir que par suite d’une grande loi de la Nature, à chaque morceau d’énergie de masse propre m, soit lié un phénomène périodique de fréquence ν telle que l’on ait : hν = mc2, ν étant mesurée dans le système lié au morceau d’énergie. Cette hypothèse est la base de notre système : elle vaut, comme toutes les hypothèses, ce que valent les conséquences qu’on en peut déduire. » [1]Plus loin dans son travail, il explique ce qui lui fait penser que ce phénomène périodique n'a pas lieu d'être considéré a priori comme confiné : il s'agirait donc d'une onde se propageant dans l'espace.
La masse m étant la masse au repos de la particule, pour être cohérent avec la définition donnée de la masse ci-dessus, on doit écrire
L'hypothèse de l'harmonie des phases ayant conduit, au paragraphe précédent, à l'expression vφv = c2 (cf p 35 de sa thèse[1]), où il l'écrit V=c/β). La longueur d’onde étant le rapport de la vitesse de phase vφ à la fréquence ν, on a :
En utilisant la quantité de mouvement :
![p=\frac{mv}{\sqrt[]{1 -\frac{v^2}{c^2}}}](/pictures/frwiki/49/14f84f070d78ff646c7e098a1620f411.png)
on obtient la relation relativiste de de Broglie :
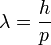
Davisson et Germer ont fait diffracter des électrons par un réseau cristallin et vérifié la formule de de Broglie de la longueur d’onde associée à des électrons monocinétiques.
En résumé, Louis de Broglie a émis l’hypothèse que pour tout corps massif de masse m, il existe une fréquence intrinsèque ν telle que hν = mc2. Par la transformation de Lorentz, de Broglie en a déduit que pour tout déplacement de cette particule à une vitesse v, se propage une onde dont la vitesse de groupe est égale à v, et la vitesse de phase vaut c²/v. La vitesse de la lumière est donc la moyenne géométrique de la vitesse de phase et de la vitesse de groupe. de Broglie a obtenu la longueur d'onde, quotient de la vitesse de phase par la fréquence. de Broglie n'a fait aucune hypothèse sur la nature de l'onde, encore inconnue, qui pourrait être gravitationnelle, électromagnétique ou autre. Actuellement, c'est l'hypothèse probabiliste de Born qui est retenue.
Il existe d'autres démonstrations possibles de l'onde de de Broglie, comme à partir des principes de Fermat et Maupertuis ou tout simplement en généralisant la formule donnant la longueur d'onde du photon :
où on remplace la vitesse c de la lumière par la vitesse v de la particule pour obtenir λ=h/mv, mais ce n'est qu'une analogie.
Références
- Portail de la physique
Catégorie : Mécanique ondulatoire
Wikimedia Foundation. 2010.

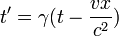
![sin[2\pi\nu'\gamma(t - \frac{vx}{c^2} )]](/pictures/frwiki/99/c3262050e371853d89fb6a43d616669e.png)
![sin[2\pi\nu'\gamma(t - \frac{x}{v_\phi})]](/pictures/frwiki/54/629be6160c608f90ebcf7acfbe64f526.png)
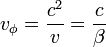
![\nu= \frac{\nu'}{ \sqrt[]{1 -\frac{v^2}{c^2}} }= \gamma\nu'](/pictures/frwiki/48/010241eaabec1f8735645a9890317c78.png)
![E=\left.h\nu=\frac{mc^2}{\sqrt[]{1 -\frac{v^2}{c^2}}} \right.](/pictures/frwiki/50/2efcd489a675bb85354462564cc2edec.png)
![\lambda= \frac{v_\phi}{\nu}= \frac{c^2}{v\nu}= \frac{h\ \sqrt[]{1 -\frac{v^2}{c^2}}}{ mv}](/pictures/frwiki/51/3f5e608483e8a3b8fc46e9f07ee87419.png)