- Apoposéide
-
Apoapside
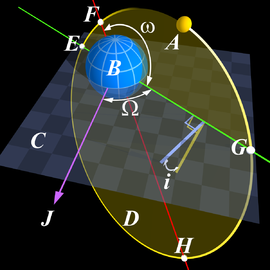 Un diagramme de Kepler des éléments orbitaux. F périapse, H apoapse, la ligne rouge entre eux est la ligne des apsides
Un diagramme de Kepler des éléments orbitaux. F périapse, H apoapse, la ligne rouge entre eux est la ligne des apsides
L'apoapse, apoapside, apside supérieure ou apocentre est le point de l'orbite d'un objet céleste où la distance est maximale par rapport au foyer de l'orbite (point "H" sur la figure ci-contre).
Son antonyme est périapside, périapse, ou péricentre (point "F" sur la figure ci-contre).
Ces deux points extrêmes (périapse et apoapse) sont désignés ensemble sous le terme générique de apsides.
Dans le cas particulier de la Terre, une confusion est à éviter :
- Si on se référe à son orbite autour du soleil, on parlera d'aphélie (prononcer apéli).
- Si on se réfère à l'orbite de ses satellites (naturel ou artificiel) autour d'elle, on parlera d'apogée.
La distance "
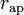 " du centre de masse à l'apoapse peut se calculer de la façon suivante :
" du centre de masse à l'apoapse peut se calculer de la façon suivante :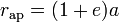
où "
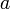 " est la longueur du demi-grand axe et "
" est la longueur du demi-grand axe et " " est l'excentricité orbitale.
" est l'excentricité orbitale.Sommaire
Formules détaillées
Article détaillé : Apsides.Les formules suivantes caractérisent le périapse et l'apoapse d'une orbite :
- Périapse :
- vitesse (maximale) du corps orbital au périapse de son orbite :
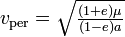
-
- distance du periapse (minimale) au centre de masse (foyer de l'orbite) :
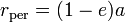
- distance du periapse (minimale) au centre de masse (foyer de l'orbite) :
- Apoapse :
- vitesse (minimale) du corps orbital à l'apoapse de son orbite :
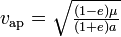
-
- distance de l'apoapse (maximale) au centre de masse (foyer de l'orbite) :
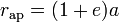
- distance de l'apoapse (maximale) au centre de masse (foyer de l'orbite) :
Selon les lois de Képler sur le mouvement des planètres (conservation du moment angulaire) et les principes de la conservation de l'énergie, les quantités suivantes sont constantes pour une orbite donnée :
- moment angulaire relatif spécifique :
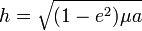
- énergie orbitale spécifique :
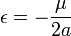
avec :
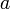 est la longueur du demi grand axe
est la longueur du demi grand axe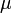 est le paramètre gravitationnel standard (produit de la constante de gravitation "grand G" par la masse "M" du corps central).
est le paramètre gravitationnel standard (produit de la constante de gravitation "grand G" par la masse "M" du corps central). est l'excentricité orbitale définie par
est l'excentricité orbitale définie par 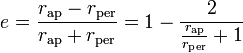
Attention : Pour convertir la distance mesurée depuis les surfaces des objets en distance mesurée depuis les centres de gravité, il faut ajouter le rayon des objets en orbite ; et réciproquement.
La moyenne arithmétique des deux distances extrêmes est la longueur du demi grand axe
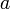 de l'ellipse orbitale. La moyenne géométrique de ces deux mêmes distances est la longuer du demi petit axe
de l'ellipse orbitale. La moyenne géométrique de ces deux mêmes distances est la longuer du demi petit axe 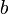 de l'ellipse orbitale.
de l'ellipse orbitale.La moyenne géométrique des deux vitesses limites
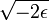 , est la vitesse correspondant à une énergie cinétique qui, à n'importe quelle position sur l'orbite, ajoutée à l'énergie cinétique courante, permettrait à l'objet en orbite de s'échapper de l'attraction. La racine carrée du produit des deux vitesses est donc la valeur locale de la vitesse de libération.
, est la vitesse correspondant à une énergie cinétique qui, à n'importe quelle position sur l'orbite, ajoutée à l'énergie cinétique courante, permettrait à l'objet en orbite de s'échapper de l'attraction. La racine carrée du produit des deux vitesses est donc la valeur locale de la vitesse de libération.Terminologie
Article détaillé : Apsides.Corps central Apoapse Galaxie Apogalacticon Trou noir Apomélasme Étoile Apoastre Soleil Aphélie Mercure Apherme Vénus Apocythère Terre Apogée Lune Aposélène Mars Apoarée Jupiter Apozène Saturne Apokrone Uranus Apourane Neptune Apoposéide Pluton Aphade Dans le cas d'une étoile ou des principaux objets du système solaire, on utilise un terme spécialisé apparenté (seuls aphélie, apogée et apoastre sont couramment utilisés).
Ces termes sont formés en prenant la racine grecque du corps correspondant.
Notez que dans Aphélie, Apherme et Aphade, la graphie "Aph" se prononcent Ap- et non Af-, le ph étant un artéfact induit par la première lettre des racines grecques désignant les corps célestes (hélios, hermès, hadès)
Les termes apolune (pour le satellite d'une lune) et apojove (pour un satellite de Jupiter) sont à éviter.
On voit parfois aussi apocynthe dans le cas d'un satellite artificiel de la Lune.
Référence
Droit français : arrêté du 20 février 1995 relatif à la terminologie des sciences et techniques spatiales.
Voir aussi
Liens internes
Lien externe
- Portail de l’astronomie
Catégorie : Orbite
Wikimedia Foundation. 2010.
