Moyenne glissante

Moyenne glissante
MovingAverage.GIF

La moyenne glissante, ou moyenne mobile, est un type de moyenne statistique utilisée pour analyser des séries ordonnées de données, le plus souvent des séries temporelles, en supprimant les fluctuations transitoires de façon à en souligner les tendances à plus long terme. Cette moyenne est dite mobile parce qu'elle est recalculée de façon continue, en utilisant à chaque calcul un sous-ensemble d'éléments dans lequel un nouvel élément remplace le plus ancien ou s'ajoute au sous-ensemble.

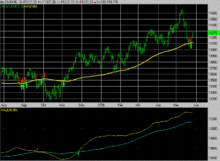
Ce type de moyenne est utilisé généralement comme méthode de lissage de valeurs, en particulier dans le domaine financier pour l'analyse technique de cours boursiers.

Mathématiquement, toute moyenne mobile est un exemple de convolution. Physiquement, une moyenne mobile est un filtre passe-bas et possède ainsi un lien profond avec le traitement du signal. En particulier, la moyenne mobile exponentielle, que nous allons aborder plus loin, est un filtre linéaire passe-bas du premier ordre tout à fait classique.

Sommaire

Moyenne mobile arithmétique

Point de vue classique

C'est une moyenne qui au lieu d'être calculée sur l'ensemble des n valeurs d'un échantillonnage, est calculée tour à tour sur chaque sous-ensemble de N valeurs consécutives (N < = n); le sous-ensemble utilisé pour calculer chaque moyenne « glisse » sur l'ensemble des données.

Par exemple, le tableau suivant montre les moyennes mobiles simples sur 3 valeurs, pour une série de 9 mesures.

Mesures 2 3 5 8 8 7 8 5 2
Moyennes glissantes néant (2 + 3 + 5)/3
3,3333		 (3 + 5 + 8)/3
5,3333		 (5 + 8 + 8)/3
7		 (8 + 8 + 7)/3
7,6666		 (8 +7 + 8)/3
7,6666		 (7 + 8 + 5)/3
6,6666		 (8 + 5 + 2)/3
5		 néant

Autre exemple; dans le cas particulier du domaine de la pollution atmosphérique, est utilisée une « moyenne glissante sur 8 heures » de la concentration d'un polluant (c'est en l'occurrence le cas de l'ozone, en objectif de qualité pour la protection de la santé humaine) ; cette moyenne pourra être calculée de 0h00 à 8h00, de 1h00 à 9h00, de 2h00 à 10h00, etc. On recherchera, sur une journée, la valeur maximale de la moyenne glissante, qui devra être inférieure à une concentration donnée. L'intérêt d'une moyenne glissante est de lisser les éventuels écarts accidentels.

Le calcul successif de moyennes mobiles pour une même suite de nombres exige de conserver toutes les valeurs utilisées par les moyennes précédentes, afin de remplacer le terme le plus ancien par le plus récent.

Une formule permettant de calculer une moyenne mobile simple est

\bar{x}_n = \frac{1}{N} \ \displaystyle{\sum_{k=0}^{N-1} \; {x_{n-k}}}\ \ ou \ \ \bar{x}_n = \bar{x}_{n-1} + \frac{ x_n - \bar{x}_{n-1} }{N}

Nature du filtre constitué par la moyenne mobile arithmétique

L'expression de gauche, ci-dessus, n'est autre qu'un produit de convolution discret entre un signal xn et une fonction porte de hauteur 1 / n. La transformée de Fourier de cette fonction est un sinus cardinal. Par conséquent, cette moyenne possède une réponse en fréquence potentiellement dérangeante, certaines variations de xn étant reportées négativement dans \bar{x}_{n} et d'autres positivement. Cela est interprétable comme un déphasage passant brusquement d'un extrême à l'autre en fonction de la vitesse de variation des données.

Moyenne mobile pondérée

Poids utilisés par une moyenne mobile pondérée de 15 valeurs.

Une moyenne pondérée est une moyenne qui utilise des coefficients pour donner un poids distinct à chaque valeur utilisée dans le calcul. Dans le cas d'une moyenne mobile pondérée, les poids de chaque terme décroissent linéairement, le plus récent ayant un poids de N et le plus ancien (le Nième) ayant un poids unitaire.

\bar{x}_{M} = { n \; p_{M} + (n-1) \; p_{M-1} + \cdots + 2 \; p_{M-n+2} + p_{M-n+1} \over n + (n-1) + \cdots + 2 + 1}

Le dénominateur est un nombre triangulaire, et peut être directement calculé comme \frac{n \; (n+1)}{2}.

Comme la moyenne mobile simple, le calcul successif de moyennes mobiles pondérées pour une même suite exige de conserver toutes les valeurs utilisées par les moyennes précédentes.

Moyenne mobile exponentielle

Point de vue classique

Poids utilisés pour les 21 plus récentes valeurs composant une moyenne mobile exponentielle de décroissance α = 0.125 (N=15).

Une moyenne mobile exponentielle utilise une pondération des termes qui décroît exponentiellement. Le poids de chaque valeur participant à la moyenne (souvent désignée par le terme observation en statistiques) est d'un facteur plus grand que la valeur qui le précède dans la série, ce qui donne plus d'importance aux observations les plus récentes, sans toutefois jamais supprimer complètement l'effet des valeurs les plus anciennes.

Une constante de lissage contrôle le degré de décroissance des poids applicables à chaque observation participant à la moyenne. Cette constante, α, est un nombre compris entre 0 et 1; elle peut être exprimée:

  • par sa valeur numérique: α = 0.1;
  • en pourcentage: α = 10% équivaut à α = 0.1;
  • en nombre de périodes: N = 19, où \scriptstyle\alpha\;=\textstyle\frac{2}{N+1}, équivaut également à α = 0.1.

Contrairement aux autres types de moyennes glissantes, le nombre de périodes N ne représente pas le nombre de valeurs participant à la moyenne; il ne sert qu'à spécifier la constante de lissage α. En effet, chaque nouveau calcul de la moyenne mobile exponentielle ajoute l'effet de la plus récente observation sans en abandonner une plus ancienne. Le poids total des N plus récentes observations utilisées par une moyenne mobile exponentielle ne constitue qu'environ 86% du poids total.

Dans sa forme la plus simple, la moyenne pondérée exponentielle s'exprime en fonction de cette même moyenne calculée lors de la précédente période. Il en existe deux formulations:

Roberts[1] (1959):   \bar{x}_{t} = \alpha \; x_{t} + (1-\alpha) \; \bar{x}_{t-1}     ——      Hunter[2] (1986):    \bar{x}_{t} = \alpha \; x_{t-1} + (1-\alpha) \; \bar{x}_{t-1}

On peut écrire différemment ces expressions pour souligner que la moyenne mobile exponentielle tend à conserver sa valeur précédente, n'en différant que par une fraction de sa différence avec la plus récente observation:

Roberts (1959):    \bar{x}_{t} = \bar{x}_{t-1} + \alpha \; ( x_{t} - \bar{x}_{t-1} )     ——      Hunter (1986):    \bar{x}_{t} = \bar{x}_{t-1} + \alpha \; ( x_{t-1} - \bar{x}_{t-1} )

Une moyenne mobile exponentielle doit être initialisée; le plus souvent, on impose \bar{x}_1 = x_{1} mais on peut également, par exemple, lui assigner une moyenne simple des 4 ou 5 premières observations. L'effet de l'initialisation de \bar{x}_1 sur les moyennes mobiles ultérieures dépend de \displaystyle\alpha; de plus grandes valeurs de la constante de lissage tendent à atténuer plus rapidement l'impact des observations plus anciennes. En effet, l'expansion de la forme de Roberts en y substituant récursivement les moyennes mobiles exponentielles des calculs précédents donne une somme infinie, mais puisque l'expression 1-α est inférieure à 1, les termes anciens sont de plus en plus petits et peuvent éventuellement être ignorés.

\bar{x}_{t} = \alpha \; \Big( x_t + (1-\alpha) \; x_{t-1} + (1-\alpha)^2 \; x_{t-2} + (1-\alpha)^3 \; x_{t-3} + \cdots \Big)
\bar{x}_{t} = \displaystyle\sum_{n=0}^{\infty} \alpha(1-\alpha)^nx_{t-n}

En posant \beta = (1-\alpha),\ \beta \in [0,1] et en remarquant que \frac{1}{\alpha} = \frac{1}{1-\beta} = 1 + \beta + \beta^2 + ... + \beta^n + ..., on a:

\bar{x}_{t} = \lim_{n \to \infty} \frac{x_t + \beta\ x_{t-1} + \beta^2\ x_{t-2}\ + ... +\ \beta^n\ x_{t-n}}{1 + \beta + \beta^2 + ... + \beta^n}

Nature du filtre constitué par la moyenne mobile exponentielle

L'expression \scriptstyle \sum_{n=0}^{\infty} \alpha(1-\alpha)^nx_{t-n}, ci-avant, n'est autre qu'un produit de convolution discret entre un signal \scriptstyle x_{t} et un filtre passe-bas du premier ordre. En effet, en écrivant \scriptstyle \alpha(1-\alpha)^n sous la forme \scriptstyle \frac{\alpha}{\ln{\frac{1}{1-\alpha}}} \ln{\frac{1}{1-\alpha}} e^{-n \ln{\frac{1}{1-\alpha}}}, on identifie la réponse impulsionnelle d'un filtre passe bas du premier ordre d'amplification \scriptstyle -\frac{\alpha}{\ln(1-\alpha)} et dont la pulsation de coupure est \scriptstyle -\ln(1-\alpha), exprimée en radians/échantillon. \scriptstyle \ln(1-\alpha) est négatif, les paramètres du filtre sont donc bien positifs.

Pour considérer des formes plus adaptées au contexte, notons que la fréquence de coupure est de \scriptstyle -\frac{\ln(1-\alpha)}{2 \pi} cycles/échantillon, soit une période de coupure de \scriptstyle -\frac{2 \pi}{\ln(1-\alpha)} échantillons. Concrètement, lorsque \scriptstyle x_{t} varie assez rapidement, lorsque \scriptstyle x_{t} fluctue en moins de \scriptstyle -\frac{2 \pi}{\ln(1-\alpha)} échantillons, la fluctuation se retrouve dans \scriptstyle \bar{x}_{t} mais est d'autant plus affaiblie qu'elle est rapide. Plus précisément, l'atténuation est de 20 dB/décade.

Par conséquent, la moyenne mobile exponentielle souffre du principal défaut des filtres passe bas classiques, à savoir un déphasage des données. Cela se traduit par un retard entre l'évolution de \scriptstyle \bar{x}_{t} et l'évolution des données \scriptstyle x_{t}, et ce retard dépend de la rapidité de l'évolution.

Autres types de moyennes

Tout comme il existe une infinité de filtres dans le domaine du traitement du signal, il existe une infinité de moyennes glissantes. Nous avons abordé dans cet article les plus courantes et avons évoqué leurs particularités dans l'espace de Fourier. Nous nous apercevons qu'elles entraînent des déphasages qui nuisent à la qualité des résultats. Nous aurions pu encore noircir le tableau en abordant les problématiques spectrales soulevées par l'échantillonnage sous-jacent aux produits de convolution discrets.

Une moyenne moins commune possède de meilleures caractéristiques. Elle se réalise par un filtre gaussien récursif. Bien qu'un filtre gaussien récursif parfait n'existe pas, il existe d'excellentes approximations d'ordre 4 grâce auxquelles seuls les défauts liés à l'échantillonnage subsistent (voir, par exemple, Deriche 1993). En effet, la transformée de Fourier d'une gaussienne est une gaussienne. Par conséquent, elle ne présente aucun déphasage, à contrario de la moyenne mobile exponentielle, et aucune oscillation, à contrario de la moyenne mobile arithmétique. Mais les calculs sont plus lourds (un filtre quasi-gaussien d'ordre 4 nécessite environ 16 opérations par valeur) et ces caractéristiques idéales ne sont rencontrées que si la moyenne est réalisée sur des données connues d'avance (un déphasage apparaît si seule la partie causale du filtre est utilisée).

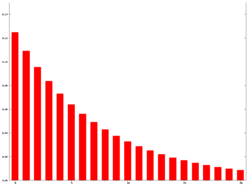
Réponses impulsionnelles

On peut voir sur le graphique ci-contre la réponse impulsionnelle pour 2 types de moyennes. On peut y lire les valeurs de la pondération utilisée, à une symétrie près (résultat Metastock v10).

Réponse à une impulsion pour des indicateurs SMA/EMA (N=20, Metastock v10)

Notes

  1. ↑ [(en) http://www.itl.nist.gov/div898/handbook/pmc/section3/pmc324.htm NIST/SEMATECH e-Handbook of Statistical Methods: EWMA Control Charts] at the National Institute of Standards and Technology
  2. ↑ [(en) http://www.itl.nist.gov/div898/handbook/pmc/section4/pmc431.htm NIST/SEMATECH e-Handbook of Statistical Methods: Single Exponential Smoothing] at the National Institute of Standards and Technology

Liens internes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Moyenne glissante de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Moyenne Glissante — La moyenne glissante, ou moyenne mobile, est un type de moyenne statistique utilisée pour analyser des séries ordonnées de données, le plus souvent des séries temporelles, en supprimant les fluctuations transitoires de façon à en souligner les… …   Wikipédia en Français

  • Moyenne (mathématiques élémentaires) — Moyenne Pour les articles homonymes, voir Valeur moyenne. La moyenne est une mesure statistique caractérisant les éléments d un ensemble de quantités : elle exprime la grandeur qu aurait chacun des membres de l ensemble s ils étaient tous… …   Wikipédia en Français

  • Moyenne générale — Moyenne Pour les articles homonymes, voir Valeur moyenne. La moyenne est une mesure statistique caractérisant les éléments d un ensemble de quantités : elle exprime la grandeur qu aurait chacun des membres de l ensemble s ils étaient tous… …   Wikipédia en Français

  • Moyenne quadratique — Moyenne Pour les articles homonymes, voir Valeur moyenne. La moyenne est une mesure statistique caractérisant les éléments d un ensemble de quantités : elle exprime la grandeur qu aurait chacun des membres de l ensemble s ils étaient tous… …   Wikipédia en Français

  • Moyenne mobile — Moyenne glissante La moyenne glissante, ou moyenne mobile, est un type de moyenne statistique utilisée pour analyser des séries ordonnées de données, le plus souvent des séries temporelles, en supprimant les fluctuations transitoires de façon à… …   Wikipédia en Français

  • Moyenne De Reynolds — Dans le cadre du traitement en mécanique des fluides de la turbulence, l utilisation de la décomposition de Reynolds appliquée aux solutions de l équation de Navier Stokes permet de simplifier le problème en faisant disparaitre les fluctuations… …   Wikipédia en Français

  • Moyenne de reynolds — Dans le cadre du traitement en mécanique des fluides de la turbulence, l utilisation de la décomposition de Reynolds appliquée aux solutions de l équation de Navier Stokes permet de simplifier le problème en faisant disparaitre les fluctuations… …   Wikipédia en Français

  • Moyenne — Pour les articles homonymes, voir Valeur moyenne. La moyenne est une mesure statistique caractérisant les éléments d un ensemble de quantités : elle exprime la grandeur qu auraient chacun des membres de l ensemble s ils étaient tous… …   Wikipédia en Français

  • Moyenne de Reynolds — Dans le cadre du traitement en mécanique des fluides de la turbulence, l utilisation de la décomposition de Reynolds appliquée aux solutions de l équation de Navier Stokes permet de simplifier le problème en faisant disparaitre les fluctuations… …   Wikipédia en Français

  • Valeur quadratique moyenne — Moyenne Pour les articles homonymes, voir Valeur moyenne. La moyenne est une mesure statistique caractérisant les éléments d un ensemble de quantités : elle exprime la grandeur qu aurait chacun des membres de l ensemble s ils étaient tous… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”