Mouvement circulaire uniforme

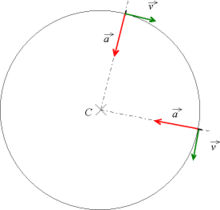
En physique, le mouvement circulaire uniforme caractérise le déplacement d'un point matériel dont la trajectoire dans le référentiel considéré est un cercle et dont la vitesse est constante.

La notion de mouvement circulaire est une notion de mécanique du point. En mécanique du solide, il faut distinguer

le mouvement de rotation, pour lequel le solide tourne autour d'un point (les points du solide décrivent des cercles concentriques), et
le mouvement de translation circulaire, pour lequel tous les points du solide décrivent des cercles de même rayon mais de centres différents, c'est celui des nacelles d'une grande roue.

Sommaire

1 Caractéristiques physiques
- 1.1 Vitesse tangentielle et accélération centripète
- 1.2 Rayon et période
2 Équations
3 Exemples
4 Notes et références
5 Annexes
- 5.1 Articles connexes
- 5.2 Bibliographie

Caractéristiques physiques

La vitesse est tangente à la trajectoire et perpendiculaire à l'accélération centripète orientée vers le centre du cercle.

Vitesse tangentielle et accélération centripète

Lors de ce type de mouvement, la vitesse tangentielle (ou linéaire) est constante en norme, mais pas en direction. Le vecteur vitesse étant par définition tangent à la trajectoire, ici circulaire, il prend à chaque instant une direction différente. Ainsi, un point décrivant une telle trajectoire à vitesse constante subit tout de même une accélération. Cette dernière, constamment orientée vers le centre du cercle autour duquel il tourne, porte le nom d'accélération centripète^[1]. Elle permet au corps de conserver sa trajectoire circulaire.

Rayon et période

Tous les points situés à même distance du centre ont la même vitesse linéaire.

Pour une même période, les points les plus éloignés du centre ont une vitesse linéaire plus élevée que les points les plus proches. Conséquemment, le temps de révolution varie en fonction de la distance qui sépare le point du centre du cercle.

Le temps nécessaire à un point donné pour effectuer une révolution complète autour du centre du cercle est qualifiée de période. La période est à la fois fonction de la vitesse du déplacement et du rayon^[2].

Équations

On se place dans le cas d'un mouvement dans le plan (x, y).

Considérons un point matériel M ayant un mouvement circulaire uniforme de centre C(x_C, y_C), de rayon r et de vitesse angulaire ω ainsi que θ₀ étant l'angle initial formé par le vecteur $\overrightarrow{\mathrm{CM}}$ et l'axe des x. Ses coordonnées suivent une équation paramétrique

$\left \{ \begin{matrix} x_{\mathrm{M}} = x_{\mathrm{C}} + r \cdot ( \cos (\omega t + \theta_0) ) \\ y_{\mathrm{M}} = y_{\mathrm{C}} + r \cdot ( \sin (\omega t + \theta_0) ) \end{matrix} \right .$ .

Soit θ l'angle que fait ce vecteur $\overrightarrow{\mathrm{CM}}$ avec l'axe des x. On a donc une vitesse angulaire constante et une accélération angulaire nulle :

$\left \{ \begin{array}{l} \alpha = \ddot{\theta} = 0 \\ \omega = \dot{\theta} = \mathrm{constante} \\ \theta = \omega t + \theta_0 \end{array} \right .$

Le vecteur vitesse a une norme constante valant

$\| \vec{v} \| = \omega \cdot r$

ou encore

$\omega = \frac{v}{r}$ .

L'accélération normale $\vec{a}_{\mathrm{n}}$ (ou accélération centripète) est constante et vaut

$a_{\mathrm{n}} = \frac{v^2}{r}$

et l'accélération tangentielle est nulle :

a t = 0

Exemples

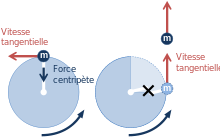La force centripète peut être causée par plusieurs phénomènes, comme la tension d'une corde. Si cette dernière se brise, la force centripète cesse d'opérer sur l'objet. On ne peut donc plus parler de mouvement circulaire uniforme. L'objet se déplace alors selon une trajectoire linéaire et parallèle à sa vitesse tangentielle au moment de la rupture^[3].

Automobile parcourant une piste circulaire

Le cas d'une automobile parcourant une piste circulaire peut être étudié comme un mouvement circulaire uniforme. Dans cette situation, l'accélération centripète est produite par la force de frottement des pneus sur la route et en partie par le poids apparent si la piste présente une certaine inclinaison.

Objets stellaires

Le mouvement de certaines planètes du système solaire présente une faible excentricité, si bien qu'il peut être considéré, en toute première approximation, comme circulaire et uniforme. Dans cette situation, c'est la force gravitationnelle qui est à l'origine de l'accélération centripète^[4].

Tourne-disque

Notes et références

↑ Benson 2009, p. 101
↑ Benson 2009, p. 103
↑ Champagne 2009, p. 158
↑ Kane et Sternheim 1986, p. 95

Annexes

Bibliographie

: Ouvrage utilisé comme source pour la rédaction de cet article

Harris Benson (trad. Marc Séguin, Benoît Villeneuve, Bernard Marcheterre et Richard Gagnon), Physique 1 Mécanique, Édition du Renouveau Pédagogique, 2009, 4^e éd., 465 p.
Joseph W. Kane et Morton M. Sternheim, Physique, Interédition, 1986, 775 p.
Marielle Champagne, Option science Physique La mécanique, Édition du Renouveau Pédagogique, 2009, 330 p.

Portail de la physique

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Mouvement circulaire uniforme de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Mouvement Circulaire Uniforme — Le mouvement circulaire uniforme caractérise le déplacement d un point matériel dont la trajectoire dans le référentiel considéré est un cercle et dont la vitesse est constante en valeur (et non en direction : le vecteur vitesse étant par… … Wikipédia en Français
Mouvement circulaire non uniforme — Le mouvement circulaire non uniforme caractérise le déplacement d un point matériel dont la trajectoire dans le référentiel considéré est un cercle et dont la vitesse est n est pas constante en valeur (ni en direction : le vecteur vitesse… … Wikipédia en Français
MOUVEMENT — Certes, la conceptualisation du mouvement ne date pas des débuts de la science moderne. Force est de constater, cependant, que la physique moderne est née à propos de la question du mouvement et en réaction, sur ce point précis, contre la… … Encyclopédie Universelle
Mouvement (mecanique) — Mouvement (mécanique) Un mouvement, dans le domaine de la mécanique (physique), est le déplacement d un corps par rapport à un point fixe de l espace et à un moment déterminé. En physique Newtonienne, on distingue : le mouvement absolu … Wikipédia en Français
Mouvement de rotation — Pour les articles homonymes, voir Rotation. Sphère en rotation autour d un de ses diamètres La rotation est l un des deux mouvements simples fondamentaux des solides, avec la translation rectiligne. En génie mécanique, il correspond au mouvement… … Wikipédia en Français
Mouvement (mécanique) — Pour les articles homonymes, voir Mouvement. Un mouvement, dans le domaine de la mécanique (physique), est le déplacement d un corps par rapport à un point fixe de l espace et à un moment déterminé. En physique Newtonienne, on distingue : le … Wikipédia en Français
uniforme — [ ynifɔrm ] adj. et n. m. • mouvement uniforme 1361; lat. uniformis, de unus et forma → forme I ♦ Adj. 1 ♦ Qui présente des éléments tous semblables; dont toutes les parties sont identiques ou perçues comme telles. Mouvement uniforme, d un corps… … Encyclopédie Universelle
circulaire — [ sirkylɛr ] adj. et n. f. • 1314; circulere XIIIe; lat. circularis I ♦ Adj. 1 ♦ Qui décrit un cercle. Mouvement circulaire. ⇒ giratoire, rotatoire. Elle « tournait sur elle même, dans un envol circulaire de la jupe » (Troyat). Regard circulaire … Encyclopédie Universelle
Rotation uniforme — Mouvement circulaire uniforme Le mouvement circulaire uniforme caractérise le déplacement d un point matériel dont la trajectoire dans le référentiel considéré est un cercle et dont la vitesse est constante en valeur (et non en direction :… … Wikipédia en Français
Mouvement brownien — d une particule. Le mouvement brownien, ou processus de Wiener, est une description mathématique du mouvement aléatoire d une « grosse » particule immergée dans un fluide et qui n est soumise à aucune autre interaction que des chocs… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Mouvement circulaire uniforme

Sommaire

Caractéristiques physiques