Modèle de Debye

En physique statistique et en physique du solide, le modèle de Debye est une explication, développée par Peter Debye en 1912^[1], du comportement de la capacité thermique des solides en fonction de la température. Il consiste à étudier les vibrations du réseau d'atomes formant le solide, autrement dit, les phonons.

Ce modèle permet d'expliquer précisément les relevés expérimentaux, alors que le modèle d'Einstein, basé sur la notion d'oscillateur harmonique quantique, présentait une légère différence. Le modèle de Debye rejoint également la Loi de Dulong et Petit à haute température.

Sommaire

1 Obtention
2 Obtention de Debye
3 Résultats du modèle
- 3.1 Limite des basses températures
- 3.2 Limite des hautes températures
4 Comparaison au modèle d'Einstein
5 Références
6 Voir aussi
- 6.1 Articles connexes
- 6.2 Liens externes

Obtention

Le modèle de Debye est analogue à l'obtention de la loi de Planck sur le rayonnement du corps noir. Le second traîte un ensemble de photons, alors que le premier traite un ensemble de phonons.

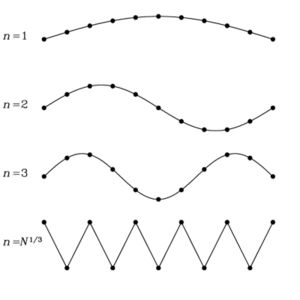
On suppose, pour simplifier, que le solide a une forme cubique de côté L. Les phonons susceptibles d'exister doivent, à la manière de la vibration d'une corde de guitare, ne pas vibrer aux extrémités (voir figure ci-contre). On en déduit alors que les longueurs d'ondes possibles sont données par :

$\lambda_n = {2L\over n}$

où n est un entier naturel non-nul.

Or l'énergie d'un phonon est donnée par :

$E_n =\hbar \omega={hc_s\over\lambda_n}={hc_s\over 2L}n$ avec $\omega=c_s |\vec k|$

où $h\,$ est la constante de Planck et $\hbar$ est la constante de Planck réduite, $\vec k$ le vecteur d'onde du phonon, et $c s$ sa vitesse.

Cela correspond, en trois dimensions, à l'expression :

$E^2 =\hbar^2 (c_s|\vec k|)^2=\left({hc_s\over 2L}\right)^2 (n_x^2+n_y^2+n_z^2)$ .

Il est alors possible de faire la somme de ces énergies pour tous les phonons présents. Pour cela, il faut utiliser la statistique de Bose-Einstein, donnant la distribution des énergies dans l'ensemble des phonons, à la température T. On obtient finalement l'expression suivante de l'énergie totale U des phonons :

$U = 9Nk_BT \left({T\over T_D}\right)^3\int_0^{T_D/T} {x^3\over e^x-1}\, dx$

où N est le nombre d'atomes dans le solide considéré, $k B$ est la constante de Boltzmann, et $T D$ est la température de Debye donnée par :

$T_D = {hc_s\over2Lk_B}\sqrt[3]{6N\over\pi}$ .

La capacité thermique molaire est alors, par définition, la dérivée de U par rapport à T. On obtient :

$C_V= 9 k_B \left({T\over T_D}\right)^3\int_0^{T_D/T} {x^4 e^x\over\left(e^x-1\right)^2}\, dx$

Obtention de Debye

En réalité, Debye a obtenu cette formule d'une façon un peu différente, et plus simple. En utilisant la mécanique des milieux continus, il montra que le nombre d'états vibrationnels accessibles aux phonons en dessous d'une fréquence $ν$ est donné approximativement par :

$n \sim {1 \over 3} \nu^3 V F$

où V est le volume du solide et F est un facteur calculé à l'aide des coefficients d'élasticité (comme le module d'Young).

En combinant cela à l'énergie d'un oscillateur harmonique (méthode déjà utilisée dans le modèle d'Einstein), on obtiendrait une énergie totale :

$U = \int_0^\infty \,{h\nu^3 V F\over e^{h\nu/k_BT}-1}\, d\nu$

Mais il ne peut pas y avoir plus d'états vibrationnels que les N atomes peuvent fournir, c'est-à-dire 3N (car il y a trois degrés de liberté de vibration par atome). Ainsi, l'intégrale de la formule précédente doit être calculée jusqu'à une fréquence maximale $ν m a x$ telle que le nombre d'états total soit 3N. C'est-à-dire :

$3N = {1 \over 3} \nu_{max}^3 V F$ .

La formule donnant l'énergie est donc :

$U = \int_0^{\nu_{max}} \,{h\nu^3 V F\over e^{h\nu/k_BT}-1}\, d\nu = 9 N k_B T \left(\frac{T}{T_D}\right) ^3 \int_0^{T_D/T} \,{x^3 \over e^x-1}\, dx$ .

On retrouve bien l'expression obtenue plus haut, avec une température $T D$ d'expression différente. On peut vérifier aussi que les deux expressions de $T D$ sont cohérentes avec la mécanique des milieux continus.

Résultats du modèle

Limite des basses températures

Lorsque la température est faible devant $T D$ , l'expression de $C V$ se simplifie :

$C_V \sim 9Nk_B \left({T\over T_D}\right)^3\int_0^{\infty} {x^4 e^x\over \left(e^x-1\right)^2}\, dx$ .

Cette intégrale peut être calculée, ce qui donne :

$C_V \sim {12\pi^4\over5}Nk_B \left({T\over T_D}\right)^3$

Les relevés expérimentaux correspondent bien à ce comportement.

Limite des hautes températures

Lorsque la température est grande devant $T D$ , l'expression de $C V$ se simplifie une fois encore :

$C_V \sim 9Nk_B \left({T\over T_D}\right)^3\int_0^{T_D/T} x^2\, dx$ .

D'où :

$C_V \sim 3Nk_B\;$

On retrouve ainsi la loi de Dulong et Petit, qui est relativement bien vérifiable par l'expérience, sauf lorsque l'anharmonicité des vibrations fait remonter la valeur de $C V$ . De plus, il peut être intéressant d'ajouter la contribution des électrons à cette capacité thermique.

Comparaison au modèle d'Einstein

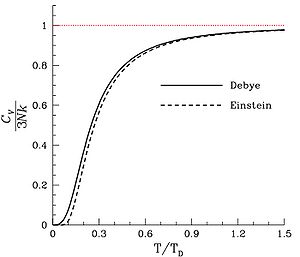
Comparaison des courbes de la capacité thermique par les modèles d'Einstein et de Debye.

Les modèles d'Einstein et de Debye donnent des résultats relativement proches, mais celui de Debye est valable aux basses températures alors que celui d'Einstein ne l'est pas.

Références

↑ 'Zur Theorie der spezifischen Warmen', Annalen der Physik 39(4), p. 789 (1912)

Voir aussi

Liens externes

Détermination expérimentale de la capacité thermique du quartz à l'aide d'un cryostat.

Portail de la physique

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Modèle de Debye de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Modele de Debye — Modèle de Debye En physique statistique et en physique du solide, le modèle de Debye est une explication, développée par Peter Debye en 1912[1], du comportement de la capacité thermique des solides en fonction de la température. Il consiste à… … Wikipédia en Français
Modèle De Debye — En physique statistique et en physique du solide, le modèle de Debye est une explication, développée par Peter Debye en 1912[1], du comportement de la capacité thermique des solides en fonction de la température. Il consiste à étudier les… … Wikipédia en Français
Modèle de debye — En physique statistique et en physique du solide, le modèle de Debye est une explication, développée par Peter Debye en 1912[1], du comportement de la capacité thermique des solides en fonction de la température. Il consiste à étudier les… … Wikipédia en Français
Modele d'Einstein — Modèle d Einstein En physique statistique et en physique du solide, le modèle d’Einstein est un modèle permettant de décrire la contribution des vibrations du réseau à la capacité calorifique d’un solide cristallin. Il est basé sur les hypothèses … Wikipédia en Français
Modèle d’Einstein — Modèle d Einstein En physique statistique et en physique du solide, le modèle d’Einstein est un modèle permettant de décrire la contribution des vibrations du réseau à la capacité calorifique d’un solide cristallin. Il est basé sur les hypothèses … Wikipédia en Français
Debye — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Peter Debye (1884 1966) est un physicien et chimiste néerlandais. Plusieurs notions sont nommées en son honneur : la longueur de Debye, une unité… … Wikipédia en Français
Modèle d'Einstein — En physique statistique et en physique du solide, le modèle d’Einstein est un modèle permettant de décrire la contribution des vibrations du réseau à la capacité calorifique d’un solide cristallin. Il est basé sur les hypothèses suivantes :… … Wikipédia en Français
DEBYE (P. J. W.) — Le physicien et physico chimiste hollandais Peter Joseph Willem Debye (Debije) a été un éminent directeur de recherches, tant en Allemagne qu’aux États Unis; il est également fort connu pour son œuvre d’écrivain scientifique. Sa théorie des… … Encyclopédie Universelle
Peter Debye — Pour les articles homonymes, voir Debye. Peter Debye Peter Debye (1912) Naissance 24 mars … Wikipédia en Français
Peter J.W. Debye — Peter Debye Peter Debye (1912) Peter Joseph William Debye (24 mars 1884 2 novembre 1966) (né Petrus Josephus Wilhelmus Debije) est un physicien et chimiste néerlandais. Sommaire … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Modèle de Debye

Sommaire

Obtention

Obtention de Debye