Mathematiques commerciales

Voici un ensemble de formules mathématiques utilisées dans différents métiers liés à l'argent — banquier, commercial, etc.

Sommaire 1 Pourcentages 2 Formation des prix 3 TVA 4 Intérêts simples 5 Intérêts composés 6 Suites arithmétiques de raison r 7 Suites géométriques de raison q 8 Escompte commercial 9 Équivalence de capitaux 10 Indice de V1 à la date t1 par rapport à V0 à la date t0

Pourcentages

• Augmentation de 25% : on multiplie par 1,25 (de manière générale, une augmentation de t% se traduit par une multiplication par )
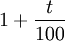• Diminution de 25% : on multiplie par 0,75 (de manière générale, une réductionde t% se traduit par une multiplication par )
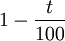• Prendre 10% de 20% : on multiplie par 0,2 puis par 0,1 (donc par 0,02, ce qui revient à prendre 2%)
• Taux de variation =
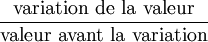
• Taux de pourcentage (ou pourcentage relatif) de a par rapport à b =

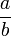
Formation des prix

• Prix d'achat net = Prix d'achat brut - Réduction
• Prix de vente net = Prix de vente brut - Réduction
• Coût d'achat = Prix d'achat net + Frais d'achat
• Coût de production = Coût d'achat + Frais de production
• Coût de revient = Coût de production + Frais de distribution
• Marge brute = Prix de vente net hors taxe - Coût d'achat
• Résultat = Prix de vente - Coût de revient (bénéfice ou perte)
• Taux de marque =
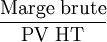
• Taux de marge =

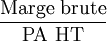
TVA

• PVTTC = PVHT + TVA
• TVA versée à l'état = TVA collectée - TVA déductible

Intérêts simples

• Valeur acquise : A = C + i
• Intérêt : i = Ctn (t taux sur une période, n nombre de périodes)
• Périodes
  • année = 360 jours
  • mois = 1/12 année = 30 jours
  • quinzaine = 1/24 année
  • jours = nb exact de jours (on compte le dernier mais pas le premier)
• Taux moyen : lorsque plusieurs capitaux sont placés à des taux différents, le taux moyen est le taux unique auquel il faudrait placer les mêmes capitaux pendant le même temps pour obtenir le même intérêt total (attention, ce n'est pas la moyenne des taux).

Intérêts composés

A = C(1 + t)ⁿ

Suites arithmétiques de raison r

• Relation de récurrence : u_{n + 1} = u_n + r
• Terme général : u_n = u₁ + (n − 1)r

Suites géométriques de raison q

• Relation de récurrence : u_{n + 1} = qu_n
• Terme général : u_n = u₁q^{n − 1}

Escompte commercial

• Valeur nominale d'un effet : somme à payer à l'échéance
• Agio = Escompte + Commissions + TVA
• Valeur nette = Valeur nominale - Agio
• Escompte : e = Vtn (V = valeur nominale)
• Valeur actuelle : a = V − e = V − Vtn = V(1 − tn)
• Taux réel d'escompte : c'est le taux T qu'il faudrait appliquer à la valeur nominale pour retrouver le montant de l'agio : Agio = VTn avec n en années. T est aussi appelé taux effectif global (TEG).

Équivalence de capitaux

• Deux capitaux placés à un même taux sont dits équivalents à une date donnée s'ils ont la même valeur actuelle à cette date.
• Un effet peut être remplacé par un autre si les deux effets sont équivalents le jour du remplacement.
• Un ensemble d'effets peut être remplacé par un effet unique si, le jour du remplacement, la valeur actuelle de l'effet de remplacement est égale à la somme des valeurs actuelles des effets remplacés.

Indice de V₁ à la date t₁ par rapport à V₀ à la date t₀

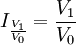
• Portail de la finance
• Portail de l’économie