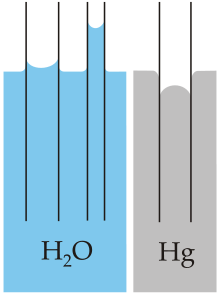
Loi de Jurin

Effet capillaire.

La loi de Jurin donne la hauteur à laquelle un liquide monte dans un tube capillaire.

Cette loi s'exprime par :

$\qquad h = \frac{2\gamma\cos(\theta)}{r.\rho.g}$

où

h est la hauteur du liquide ;
γ est la tension superficielle du liquide ;
θ est l'angle de raccordement entre le liquide et la paroi du tube, généralement appelé angle de contact ;
ρ est la masse volumique du liquide ;
r est le rayon du tube ;
g est l'accélération de la pesanteur.

Les conditions de validité sont les suivantes : il faut que le diamètre du tube soit petit devant la longueur capillaire, qui vaut typiquement deux millimètres pour de l'eau à la température et pression ambiante. Si le tube est tenu oblique alors la loi de Jurin donne la hauteur verticale (pas la hauteur mesurée le long du tube).

Justification de la loi de Jurin

La hauteur $h$ à laquelle monte le liquide dans le tube est telle que la pression dans le liquide situé immédiatement sous le ménisque obéit simultanément à deux lois : la loi hydrostatique dans le tube et la loi de Laplace-Young à travers l'interface que constitue le ménisque.

Hydrostatique

Dans le récipient, juste en-dessous de la surface du liquide, la pression dans le liquide est égale à la pression atmosphérique $p atm$ . Lorsque le liquide forme un ménisque dans le tube à une hauteur $h$ au-dessus de la surface dans le récipient, la pression dans le liquide juste en-dessous du ménisque est donc plus basse, et l'écart de pression est donné par la pression hydrostatique. Ainsi, la pression sous le ménisque vaut :

$p atm - ρ. g . h$

Pression de Laplace

Si le tube est de section circulaire (rayon $r$ ) et si l'on suppose que le ménisque a une forme sphérique (voir la discussion plus bas), alors le rayon de courbure du ménisque vaut $R = r / cos θ$ , où $θ$ est l'angle de contact.

Du fait de la tension superficielle au sein de l'interface air/liquide, cette courbure de la surface du ménisque donne lieu à une différence de pression $2γ / R$ entre l'air et le liquide (c'est la loi de Laplace-Young).

Puisque la pression dans l'air vaut $p atm$ , la pression dans le liquide immédiatement en-dessous du ménisque vaut donc :

$p_{\rm atm} - \frac{2\gamma.\cos\theta}{r}$

Loi de Jurin

En combinant les relations obtenues ci-dessus, on obtient :

$\rho.g.h = \frac{2\gamma.\cos\theta}{r}$ ,

ce qui constitue la loi annoncée.

Limites de la loi de Jurin

Ascension du liquide, rayon du tube et longueur capillaire

Dans la limité d'un tube très large, un ménisque se forme sur tout le périmètre intérieur (et extérieur) du tube. Hormis dans ce ménisque, la surface du liquide est plane et horizontale presque partout à l'intérieur du tube. Cette surface intérieure plane est au même niveau que la surface du liquide à l'extérieur du tube. Autrement dit, le liquide ne monte pas dans le tube.

Cette situation se produit lorsque la largeur du ménisque est très inférieure au rayon du tube. Or, la largeur d'un ménisque est de l'ordre de la longueur capillaire, qui vaut $\sqrt{\frac{\gamma}{\rho.g}}$ .

Ainsi, la loi de Jurin est valide uniquement si :

$r\ll\sqrt{\frac{\gamma}{\rho.g}}$

Forme sphérique du ménisque

Dans un tube circulaire, le ménisque est de forme sphérique uniquement si sa courbure est partout la même. Or, selon la loi de Laplace-Young, cela signifie que la différence de pression entre l'air et le liquide est partout la même. L'air étant beaucoup moins dense que le liquide, cela signifie plus précisément que la pression dans le liquide immédiatement sous la surface du ménisque est partout la même.

Cela n'est évidemment pas rigoureusement le cas puisque le bord du ménisque (autrement dit la ligne triple) est situé à une distance $δ$ au-dessus du centre du ménisque, donnée par :

$\delta= R (1-\sin\theta) = r \frac{1-\sin\theta}{\cos\theta}$

La courbure peut être considérée comme constante si cette différence de hauteur $δ$ est négligeable devant la différence de hauteur avec la surface à l'extérieur de tube, autrement dit si l'on a :

$\delta\ll h$

Autrement dit :

$r\ll\frac{\cos\theta}{\sqrt{1-\sin\theta}}\sqrt{\frac{\gamma}{\rho.g}}$

Si cette condition n'est pas respectée (par exemple la surface d'un liquide dans une assiette ronde), la courbure du ménisque n'est plus du tout constante (la surface n'est plus sphérique) mais suit, depuis le centre de l'assiette vers les bord, une progression monotone croissante qu'on peut mieux approximer (dans un plan de coupe passant par l'axe normal au centre de la surface) par un arc de clothoïde (courbe formée qui suppose que cette progression monotone de la courbure est linéaire selon la distance depuis le centre du ménisque). On observe alors facilement une élévation visible du ménisque uniquement près des bords, alors que sur la plus grande partie de la surface cette différence d'élévation est négligeable et imperceptible (et même quasi nulle au centre du ménisque, et en tout cas très nettement inférieure à l'élévation que prédirait la loi de Jurin, qui n'est donc plus applicable).

Forme du tube

Si le tube n'est pas circulaire ou s'il est penché, la surface du ménisque n'a plus la symétrie de révolution. La loi de Laplace-Young demeure valide mais permet alors seulement d'exprimer la courbure totale de la surface en chaque point du ménisque. La forme exacte du ménisque doit alors être calculée entièrement, en tenant compte des conditions de raccordement à la paroi du tube.

Voir aussi

Regardez d'autres dictionnaires:

Loi De Jurin — Effet capillaire. La loi de Jurin donne la hauteur à laquelle un liquide monte dans un tube capillaire. Cette loi s exprime par … Wikipédia en Français
Loi de jurin — Effet capillaire. La loi de Jurin donne la hauteur à laquelle un liquide monte dans un tube capillaire. Cette loi s exprime par … Wikipédia en Français
Loi scientifique — Liste des lois scientifiques Liste des lois scientifiques par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom de la loi comprend des noms de scientifiques, on se base sur le premier… … Wikipédia en Français
INTERFACES — Une interface peut être définie, de la façon la plus générale, comme étant la zone qui sépare deux milieux A et B. Ces milieux doivent différer par au moins une des propriétés suivantes: – composition chimique; – nature des phases: solides,… … Encyclopédie Universelle
FLUIDES (MÉCANIQUE DES) — La mécanique des fluides constitue l’extension de la mécanique rationnelle à une classe de milieux continus dont les déformations peuvent prendre des valeurs aussi grandes que l’on veut. On désigne sous le nom général de fluides des corps… … Encyclopédie Universelle
Brasage — Le brasage des métaux est un procédé d assemblage permanent qui établit une continuité métallique entre pièces réunies. Le mécanisme du brasage est la diffusion / migration atomique de part et d autre des bords à assembler (substrat) obtenue par… … Wikipédia en Français
Tension superficielle — La tension superficielle permet à un pengő hongrois en aluminium de ne pas couler au fond du verre d eau (bien que l aluminium soit plus dense que l eau)… … Wikipédia en Français
Tension de surface — Tension superficielle La tension superficielle permet à un pengő hongrois (aluminium) de ne pas couler au fond du verre d eau À la surface d un milieu dense (liquide ou solide) ou à l interface entre deux milieux denses, la matière n est pas,… … Wikipédia en Français
Énergie de surface — Tension superficielle La tension superficielle permet à un pengő hongrois (aluminium) de ne pas couler au fond du verre d eau À la surface d un milieu dense (liquide ou solide) ou à l interface entre deux milieux denses, la matière n est pas,… … Wikipédia en Français
Liste Des Lois Scientifiques — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom de la loi comprend des noms de scientifiques, on se base sur le premier nom propre cité. Si le nom de la loi ne comprend pas de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Loi de Jurin

Sommaire