- Logique Épistémique
-
Logique épistémique
La logique épistémique est la logique de la connaissance d'agents pris individuellement. Son nom vient du verbe grec epistémei qui signifie savoir, qui a aussi produit le mot épistémologie. Ses créateurs sont E. J. Lemmon and Jaakko Hintikka. Elle est complétée par la logique de la connaissance commune qui met en œuvre plusieurs agents.
L'application de la logique épistémique à l'économie a été promue par Robert Aumann, « Prix Nobel » d'économie 2005.
En logique épistémique il y a plusieurs agents qui ont la capacité de raisonner en prenant en compte la connaissance qu'ils ont de certaines propositions ou la connaissance des autres agents. C'est typiquement la logique d'un joueur qui raisonne sur son jeu.
La logique épistémique règle donc les aspects logiques ayant trait à la connaissance d'un agent. Ici nous ne présentons que la logique épistémique propositionnelle. Il existe une modalité Ki pour chaque agent i. Ainsi Ki(φ) signifie que l'agent i sait φ. La logique épistémique est donc une logique modale
Sommaire
Les règles et les axiomes
La logique épistémique se formalise plus facilement en utilisant une approche à la Hilbert (les seules formules auxquelles on s'intéresse sont les théorèmes). Dans ce qui suit
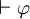doit se lire «
est un théorème». La logique épistémique satisfait les axiomes de la logique modale, mais avec une signification différente (voir ci-dessus). Certains philosophes n'acceptent que certains parmi les axiomes qui suivent, notamment parmi T, 4 et 5.Les règles
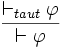Tautologie où 
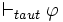signifie que est une tautologie classique (ou intuitionniste).
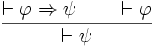modus ponens
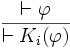règle de nécessitation ou de généralisation
Les axiomes
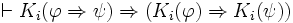axiome de distribution ou axiome K.
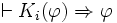axiome de la connaissance ou axiome T ou encore axiome de vérité.
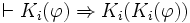axiome d'introspection positive ou 4.
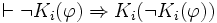axiome d'introspection négative ou 5.
La signification des règles et des axiomes
La règle Tautologie dit que toutes les propositions qui sont des théorèmes (c'est-à-dire des tautologies) de la logique classique (ou intuitionniste) sont des théorèmes de la logique épistémique.
Le modus ponens est la règle bien connue depuis Aristote qui permet de faire des déductions.
La règle de généralisation signifie que les agents raisonnent parfaitement et sont à même de connaître tous les faits pour lesquels il existe une démonstration.
L'axiome K montre comment l'agent peut faire des déductions à partir de ce qu'il connaît.
L'axiome T dit que les agents ne connaissent que des choses «vraies», autrement dit, si un agent connaît quelque chose alors cette chose est vraie.
L'axiome 4 dit que si un agent sait quelque chose, alors il sait qu'il le sait.
L'axiome 5 dit que si un agent ne sait pas quelque chose, alors il sait qu'il ne le sait pas.
T, S4 et S5
La logique
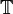est formée des règles et des axiomes K et T. La logique 
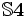est 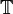augmentée de 4. La logique 
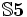est 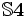augmentée de 5.Les modèles
Les modèles de la logique épistémique sont des modèles de Kripke adaptés spécifiquement aux modalités Ki.
Présentation intuitive
L'idée de Kripke est que chaque agent imagine des mondes dans lesquels telle ou telle proprosition est réalisée et telle ou telle autre ne l'est pas. En fonction du monde où l'agent se trouve, tel autre monde lui paraît possible ou impossible. Donc pour chaque agent dans un monde donné, certains mondes lui paraissent accessibles à son imagination d'autres pas. La relation qui relie les mondes entre eux est la relation d'accessiblité. Il y a une relation d'accessiblité pour chaque agent. S'il y a n agents, il y a donc n relations d'accessiblité étiquettée chacune par le nom de l'agent.
On définit enfin une relation de réalisabilité entre un monde et une proposition. Un monde réalise la proposition
siginfiera que la proposition se trouve être «vraie» dans ce monde.Présentation formelle
Dans un modèle de Kripke, on distingue:
- un univers
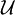dont les éléments notés m sont appélés des mondes,
- pour chaque agent i une relation
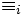dite relation d'accessibilité pour i,
- une relation
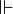de réalisabilité entre un monde m et une proposition , on écrit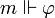 
et on lit m réalise .
Un cône est un ensemble C de mondes (
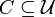) tels- si
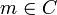
- et si pour tout i entre 1 et n, on a
,
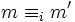alors
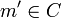.Une intitalisation est une application I qui associe à chaque variable un cône de
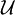.Le triplet
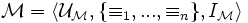s'appelle un modèle ou une structure de Kripke. S'il n'y a pas d'ambiguïté on abandonne les indices 
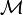.La relation de réalisabilité, notée
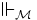, ou 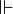quand il n'y a pas d'ambiguïté, se définit par induction sur la structure des propositions.- Si est une variable x,
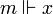si et seulement si 
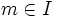. - Si
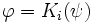, alors 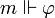si et seulement pour tout monde 
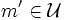tel que 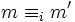on a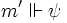 
. - Si
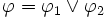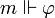, si et seulement si 
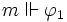ou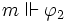 
. - Et ainsi de suite pour chaque connecteur.
On dit que
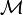est valide dans ou que 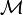modélise , noté 
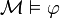, si pour 
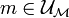, on a 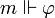.Validité
Une proposition
est valide (noté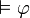 
) si pour tout modèle 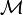on a 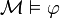. Autement dit, une proposition est valide si pour tout modèle 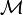et tout monde m dans ce modèle, 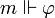.Théorème de correction
Toute proposition prouvable est valide. Autrement dit, si
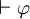alors 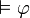Complétude
Complétude de T
Si l'on considère les modèles où les relations d'accessibilité sont réflexives alors toute proposition valide est prouvable dans
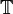.Complétude de S4
Si l'on considère les modèles où les relations d'accessibilité sont des relations de préordre (réflexives et transitives) alors toute proposition valide est prouvable dans
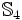.Complétude de S5
Si l'on considère les modèles où les relations d'accessibilité sont des relations d'équivalence (réflexives, transitives et symétriques) alors toute proposition valide est prouvable dans
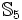.Sources
- J-J Ch. Meyer and W van der Hoek Epistemic Logic for Computer Science and Artificial Intelligence, volume 41, Cambridge Tracts in Theoretical Computer Science, Cambridge University Press, 1995. ISBN 052146014X
- R. Fagin, J. Y. Halpern, Y. Moses, and M. Y. Vardi. Reasoning about Knowledge, The MIT Press, 1995. ISBN 0-262-56200-6
Portail de la logique
Portail de la philosophie
Catégories : Logique modale | Logique mathématique
Wikimedia Foundation. 2010.
