Limite de Betz

Pour les articles homonymes, voir Betz.

Traversée d'un capteur de surface S par un fluide.

La limite de Betz est une loi physique qui indique que la puissance théorique maximale développée par un capteur éolien est égale à 16/27 de la puissance incidente du vent qui traverse l'éolienne.

Sommaire

1 Historique et énoncé
2 Démonstration
3 Limite théorique et implication pratique de la formule
4 Interprétation physique
5 Notes et références
6 Voir aussi

Historique et énoncé

Ce résultat fut découvert par l'allemand Albert Betz en 1919 et fut publié dans son livre Wind Energie en 1926. Cette loi s'applique à tout type d'éolienne que l'on désignera d'ailleurs par le nom générique de capteur éolien.

Betz calcule que

la puissance théorique maximale récupérable par un capteur éolien est égale à 16/27 de la puissance incidente du vent qui traverse l'éolienne ;
cette limite sera atteinte lorsque la vitesse du vent sera divisée par trois entre l'amont et l'aval de l'éolienne.

La puissance incidente du vent est cinétique et dépend de la surface que le capteur éolien propose au vent, de la vitesse du vent et de la masse volumique de l'air. On peut regrouper ces résultats selon ces formules :

$P_{extraite}^{max}=\frac{16}{27}.P_{incidente}$ avec $P_{incidente} = P_{cinetique} = \frac{1}{2}.\rho.S.v_{amont}^3 \,$

lorsque $v_{aval} = \frac{1}{3} v_{amont}$

ρ

: masse volumique du fluide (1,23 kg/m³ pour l'air à 20°C)

S : surface du capteur éolien en m²

v a m o n t

: vitesse incidente (amont) du fluide en m/s

Démonstration

Cette démonstration repose sur les équations fondamentales de la mécanique des fluides (théorème de Bernoulli, théorème d'Euler).

Modélisation

- écoulement monodimensionnel par section, stationnaire d'un fluide parfait homogène

- on se place dans le référentiel terrestre supposé galiléen

Notation

ρ

: masse volumique du fluide

g : accélération de la pesanteur

S : surface du capteur éolien

pour toutes les variables suivantes, l'indice

1

correspond à l'entrée du capteur et l'indice

2

correspond à la sortie

s

: section occupée par le flux d'air capté (variable, voir plus bas)

p

: pression

v

: vitesse de l'air

Dm : débit massique d'air,

D m = ρ s v

F

: force exercée par l'air sur le capteur

P

: puissance développée par la force exercée.

Calculs

Dans le cas examiné le débit massique est constant : $D m = ρ s v = c s t e$ ^[1].

Considérons quatre points sur une même ligne de courant : un point en amont (sur $s 1$ ), un point "juste avant" le capteur proprement dit, un autre "juste après", et un dernier en aval (sur $s 2$ ) :

Aux deux points loin du capteur, sur $s 1$ et $s 2$ , la pression est égale à la pression atmosphérique $p 0$

Aux deux points proches du capteur, la section est égale à la surface S, comme le débit massique est constant la vitesse du vent est la même en ces deux points : $v$ . En revanche il y a une discontinuité de pression entre ces deux points.

L'écoulement est supposé parfait et stationnaire, et le fluide est supposé incompressible (masse volumique constante) ; l'effet du champ de pesanteur est nul (l'air capté flotte dans l'air "autour", la poussée d'Archimède équilibre exactement le poids de l'air, dont l'éventuel travail - même en supposant une variation d'altitude - est ainsi annulé). On applique le théorème de Bernoulli deux fois, d'une part entre l'amont et le point juste avant, d'autre part le point juste après et l'aval ; on a donc :

(1) : $\frac {p_{0}}{\rho}+\frac {v_{1}^2}{2}=\frac {p_1}{\rho}+\frac {v^2}{2}$

(2) : $\frac {p_{0}}{\rho}+\frac {v_{2}^2}{2}=\frac {p_2}{\rho}+\frac {v^2}{2}$

La soustraction (1) - (2) donne

(3) : $p_1 - p_2 = \frac {\rho}{2}(v_{1}^2 - v_{2}^2)$

La force exercée par le vent sur le capteur est

(4) : $F = (p_1 - p_2).S = \frac {\rho}{2}(v_{1}^2 - v_{2}^2).S = \rho.S.\frac {(v_{1}+ v_{2})}{2}(v_{1}- v_{2})$

Mais cette force peut aussi s'exprimer par application de la loi de Newton :

(5) : $\begin{align} F & = m \cdot a \\ & = m \cdot \tfrac {dv} {dt} \\ & = Dm \cdot \Delta v \\ & = \rho \cdot S \cdot v \cdot \left ( v_1 - v_2 \right ) \\ \end{align}$

L'égalité des deux expressions (4) et (5) implique que $v = \frac {(v_{1}+ v_{2})}{2}$ et la puissance développée par cette force est

(6) : $P = F.v = \frac {\rho}{2}(v_{1}^2 - v_{2}^2).S.v$ ;

Si on exprime cette puissance en fonction de $x=\frac {v_{2}}{v_{1}}$ , du rendement r, et de $P 0$ la puissance incidente du vent non perturbé :

$P_{0}=\frac{1}{2} \rho S v_{1}^3$

on obtient

$v = v_1\frac{1+x}{2}$

$r=\frac {P}{P_{0}}=\frac{1}{2}(1-x^2)(1+x)$

On peut alors tracer le rendement r de l'éolienne en fonction de x :

Le maximum^[2] est atteint pour x=1/3, et alors r=16/27. D'où la limite de Betz :

$P_{extraite}^{max} \,\, = \,\, \frac {16}{27} \, P_{incidente}$

Limite théorique et implication pratique de la formule

le calcul suppose qu'on néglige l'énergie thermique contenue dans le fluide, et que la masse volume de ce fluide reste constante. Or l'extraction d'énergie cinétique aura des effets thermiques sur le fluide, qui peut à son tour faire évoluer la masse volumique (condensation de vapeur d'eau par exemple). Ce phénomène d'importance faible pour l'air, il peut être non négligeable dans d'autre cas. La limite de Betz s'applique à tout type d'éolienne, mais elle ne s'applique pas à une turbine à vapeur par exemple.

le calcul fait un certain nombre d'hypothèse qui font de ce maximum un majorant, et non un maximum atteignable ; des calculs modernes plus élaborés^[3]^,^[4] montrent que le maximum est plus bas.

à la limite de Betz, le vent voit sa vitesse divisée par trois ; pour maintenir le même débit, la surface de sortie doit donc être multipliée par trois.

on voit que la courbe du rendement est assez plate, ce qui signifie que le rendement reste assez bon même quand on s'éloigne significativement de l'optimum.

Interprétation physique

L'existence de la limite de Betz traduit la compétition entre deux phénomènes opposés :

Une éolienne récupère d'autant plus d'énergie qu'elle freine plus le vent (ce qui est traduit par le terme $(v_{1}^2-v_{2}^2)$ de la formule de puissance) ...
... mais elle en récupère d'autant moins le débit est plus faible, or le ralentissement réduit le débit (ce qui est traduit par le terme $(v 1 + v 2)$ de la formule de puissance)

Notes et références

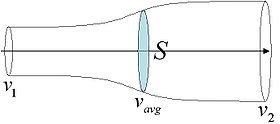
↑ remarque : Le capteur éolien capte l'énergie cinétique du vent, cela réduit la v vitesse du vent et donc parallèlement s augmente de la même proportion, d'où la figure ci-dessous représentant le tube de courant (bleu) dans lequel est plongé le capteur éolien.
↑ Pour rechercher le maximum d'une fonction, on recherche les points où sa dérivée s'annule
↑ Gorban' A.N., Gorlov A.M., Silantyev V.M., Limits of the Turbine Efficiency for Free Fluid Flow, Journal of Energy Resources Technology - December 2001 - Volume 123, Issue 4, pp. 311-317.
↑ Hartwanger, D., Horvat, A., 3D Modelling of A Wind Turbine Using CFD, NAFEMS UK Conference 2008 "Engineering Simulation: Effective Use and Best Practice", Cheltenham, UK, June 10–11, 2008, Proceedings.

Voir aussi

Catégorie :

Énergie éolienne

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Limite de Betz de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Limite De Betz — La limite de Betz est une loi physique qui indique que la puissance théorique maximale récupérable par un capteur éolien est égale à 16/27 de la puissance incidente du vent qui traverse l éolienne. Sommaire 1 Historique et énoncé 2 Démonstration… … Wikipédia en Français
Limite de betz — La limite de Betz est une loi physique qui indique que la puissance théorique maximale récupérable par un capteur éolien est égale à 16/27 de la puissance incidente du vent qui traverse l éolienne. Sommaire 1 Historique et énoncé 2 Démonstration… … Wikipédia en Français
Betz — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Betz est un nom de famille et un nom de lieu. Patronyme Vladimir Betz (1834 1894), anatomiste et histologiste russe. (en:Vladimir Betz) Albert Betz (1885… … Wikipédia en Français
Bazoches-sur-le-Betz — Pour les articles homonymes, voir Bazoches (homonymie). 48° 08′ 01″ N 2° 59′ 14″ E … Wikipédia en Français
Effort sur une voile — Exemple d effort du vent sur différents types de voile de voiliers classiques lors d une régate à Cannes en 2006. Le principe d une voile est de récupérer l énergie du vent et de la transmettre au bateau. L effet propulsif est réparti sur toute… … Wikipédia en Français
ÉNERGIES RENOUVELABLES — Les énergies renouvelables utilisent des sources inépuisables d’énergies d’origine naturelle: rayonnement solaire, vents, cycles de l’eau et du carbone dans la biosphère, flux de chaleur interne de la Terre, effet de l’attraction lunaire et… … Encyclopédie Universelle
Éolienne — Pour les articles homonymes, voir Éolienne (homonymie). Une éolienne est un dispositif qui transforme l énergie cinétique du vent en énergie mécanique puis, éventuellement, en énergie électrique. Les éoliennes produisant de l électricité sont… … Wikipédia en Français
Energie hydrolienne — Hydrolienne Une hydrolienne est une turbine sous marine (ou subaquatique, ou posée sur l eau et à demi immergée) qui utilise l énergie cinétique des courants marins ou de cours d eau, comme une éolienne utilise l énergie cinétique de l air. La… … Wikipédia en Français
Hydraulienne — Hydrolienne Une hydrolienne est une turbine sous marine (ou subaquatique, ou posée sur l eau et à demi immergée) qui utilise l énergie cinétique des courants marins ou de cours d eau, comme une éolienne utilise l énergie cinétique de l air. La… … Wikipédia en Français
Hydrolienne — (vue d artiste) Une hydrolienne est une turbine sous marine (ou subaquatique, ou posée sur l eau et à demi immergée) qui utilise l énergie cinétique des courants marins ou de cours d eau, comme une éolienne utilise l énergie cinétique de l air.… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Limite de Betz

Sommaire

Historique et énoncé