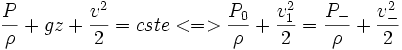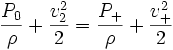Limite de betz

Limite de betz

Limite de Betz

La limite de Betz est une loi physique qui indique que la puissance théorique maximale récupérable par un capteur éolien est égale à 16/27 de la puissance incidente du vent qui traverse l'éolienne.

Sommaire

Historique et énoncé

Ce résultat fut découvert par l'allemand Albert Betz en 1919 et fut publié dans son livre Wind Energie en 1926. Aussi surprenant que cela puisse paraître, cette loi s'applique à tout type d'éolienne (exception faite des éoliennes à axe vertical comme celle de http://www.eolprocess.com/ et à rotor de Savonius) que l'on désignera d'ailleurs par le nom générique de capteur éolien.

En effet, Betz affirme que la puissance théorique maximale récupérable par un capteur éolien est égale à 16/27 de la puissance incidente du vent qui "traverse" l'éolienne. Il affirme de plus que cette limite sera atteinte lorsque le capteur éolien freinera le vent à 1/3 de sa vitesse en amont de l'éolienne. Bien entendu, la puissance incidente du vent est cinétique et dépend de la surface que le capteur éolien "propose au vent", de la vitesse du vent et de la masse volumique de l'air. On peut regrouper ces résultats selon ces formules :

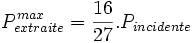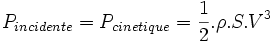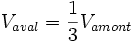
P_{extraite}^{max}=\frac{16}{27}.P_{incidente} avec P_{incidente} = P_{cinetique} = \frac{1}{2}.\rho.S.V^3 \, lorsque V_{aval} = \frac{1}{3} V_{amont}
ρ : masse volumique du fluide (1.23 kg/m³ pour l'air à 20°C)
S : surface du capteur éolien en m²
V : vitesse incidente (amont) du fluide en m/s

Démonstration

Pour se lancer dans cette démonstration, il faut avoir une idée de ce que sont le théorème de Bernoulli, le théorème d'Euler... un minimum de connaissances de mécanique des fluides.

Modélisation

- écoulement monodimensionnel par section, stationnaire d'un fluide parfait homogène
- on se place dans le référentiel terrestre supposé galiléen

Notation

- Dm : débit massique d'air
- S : surface du capteur éolien
- ρ : masse volumique du fluide

Selon le modèle, le débit massique est constant Dm = ρSv = cste, mais v diminue car le capteur éolien capte l'énergie cinétique du vent, on en déduit que S augmente, d'où la figure ci-dessous représentant le tube de courant (bleu) dans lequel est plongé le capteur éolien.

Un bilan de quantité de mouvement permet alors d'exprimer l'effort F transmis au rotor : F = Dm(v1 − v2) (1)

Maintenant considérons le tube de courant au niveau du rotor de l’éolienne, l'écoulement est supposé parfait et stationnaire, on néglige le champ de pesanteur et on suppose le fluide incompressible, on peut alors utiliser le théorème de Bernoulli sur une même ligne de courant entre S1 et l’amont du rotor, et entre S2 et l’aval du rotor :

\frac {P}{\rho}+gz+\frac {v^2}{2}=cste <=> \frac {P_{0}}{\rho}+\frac {v_{1}^2}{2}=\frac {P_{-}}{\rho}+\frac {v_{-}^2}{2}
\frac {P_{0}}{\rho}+\frac {v_{2}^2}{2}=\frac {P_{+}}{\rho}+\frac {v_{+}^2}{2}

Donc, lorsque ε − > 0 on aura v + = v − = v, on en déduit alors : 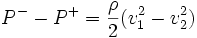P^--P^+=\frac {\rho}{2}(v_{1}^2 - v_{2}^2) (2)

Et en faisant un bilan de quantité de mouvement sur ce second contour on obtient : − F + S(P + − P − ) = Dm(v + − v − ) = 0 (3)

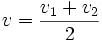
On tire alors des relations (1) (2) et (3) : v=\frac{v_{1}+v_{2}}{2}

Maintenant en notant P la puissance extraite par le capteur éolien et P0 la puissance incidente du vent non perturbé :

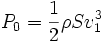
P_{0}=\frac{1}{2} \rho S v_{1}^3

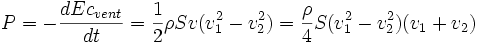
P=-\frac{dEc_{vent}}{dt}=\frac {1}{2} \rho S v (v_{1}^2-v_{2}^2)=\frac{\rho}{4} S (v_{1}^2-v_{2}^2)(v_{1}+v_{2})

On peut alors tracer le rendement r de l'éolienne en fonction de x défini par :

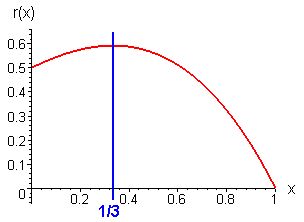
Ratio.gif

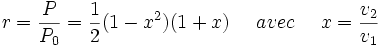
r=\frac {P}{P_{0}}=\frac{1}{2}(1-x^2)(1+x) \,\,\,\,\,\,\,\, avec \,\,\,\,\,\,\,\, x=\frac {v_{2}}{v_{1}}

On remarque alors que l'on atteint un maximum pour x=1/3, alors r=16/27 d'où la limite de Betz :

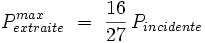
P_{extraite}^{max} \,\, = \,\, \frac {16}{27} \, P_{incidente}

Source

  • Portail de l’énergie Portail de l’énergie
Ce document provient de « Limite de Betz ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Limite de betz de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Limite De Betz — La limite de Betz est une loi physique qui indique que la puissance théorique maximale récupérable par un capteur éolien est égale à 16/27 de la puissance incidente du vent qui traverse l éolienne. Sommaire 1 Historique et énoncé 2 Démonstration… …   Wikipédia en Français

  • Limite de Betz — Pour les articles homonymes, voir Betz. Traversée d un capteur de surface S par un fluide. La limite de Betz est une loi physique qui indique que la puissance théorique maximale dé …   Wikipédia en Français

  • Betz — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Betz est un nom de famille et un nom de lieu. Patronyme Vladimir Betz (1834 1894), anatomiste et histologiste russe. (en:Vladimir Betz) Albert Betz (1885… …   Wikipédia en Français

  • Bazoches-sur-le-Betz — Pour les articles homonymes, voir Bazoches (homonymie). 48° 08′ 01″ N 2° 59′ 14″ E …   Wikipédia en Français

  • Effort sur une voile — Exemple d effort du vent sur différents types de voile de voiliers classiques lors d une régate à Cannes en 2006. Le principe d une voile est de récupérer l énergie du vent et de la transmettre au bateau. L effet propulsif est réparti sur toute… …   Wikipédia en Français

  • ÉNERGIES RENOUVELABLES — Les énergies renouvelables utilisent des sources inépuisables d’énergies d’origine naturelle: rayonnement solaire, vents, cycles de l’eau et du carbone dans la biosphère, flux de chaleur interne de la Terre, effet de l’attraction lunaire et… …   Encyclopédie Universelle

  • Éolienne — Pour les articles homonymes, voir Éolienne (homonymie). Une éolienne est un dispositif qui transforme l énergie cinétique du vent en énergie mécanique puis, éventuellement, en énergie électrique. Les éoliennes produisant de l électricité sont… …   Wikipédia en Français

  • Energie hydrolienne — Hydrolienne Une hydrolienne est une turbine sous marine (ou subaquatique, ou posée sur l eau et à demi immergée) qui utilise l énergie cinétique des courants marins ou de cours d eau, comme une éolienne utilise l énergie cinétique de l air. La… …   Wikipédia en Français

  • Hydraulienne — Hydrolienne Une hydrolienne est une turbine sous marine (ou subaquatique, ou posée sur l eau et à demi immergée) qui utilise l énergie cinétique des courants marins ou de cours d eau, comme une éolienne utilise l énergie cinétique de l air. La… …   Wikipédia en Français

  • Hydrolienne — (vue d artiste) Une hydrolienne est une turbine sous marine (ou subaquatique, ou posée sur l eau et à demi immergée) qui utilise l énergie cinétique des courants marins ou de cours d eau, comme une éolienne utilise l énergie cinétique de l air.… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”