- Lentille Asphérique
-
Lentille asphérique
On appelle objet asphérique un objet dont la forme est proche d'une portion de sphère, mais non strictement sphérique.
Dans le domaine de l'optique, les lentilles modernes sont souvent asphériques.
En effet, les lentilles de forme traditionnelle sont de forme sphérique, ce qui conduit à des aberrations optiques. Par exemple, les rayons qui passent par le centre ne convergent pas tout-à-fait au même point que ceux qui passent par les bords, ce qui provoque du flou aux grandes ouvertures.
Une lentille asphérique bien calculée n'est pas affectée par ce phénomène.
La généralisation des lentilles asphériques a entrainé une augmentation spectaculaire des performances des objectifs photographiques à bon marché, une seule lentille moulée suffit pour obtenir une image très correcte, et ce à toutes les focales ; dans le segment du haut de gamme, elles ont permis de diminuer drastiquement le nombre de lentilles, surtout dans le cas des zooms, tout en améliorant, là aussi notablement, les performances.
Équation d'une lentille asphérique
La flèche z d'une lentille asphérique en fonction de la distance à l'axe optique r dépend de deux paramètres : le rayon de courbure R (ou la courbure C = 1/R) et la conicité K.
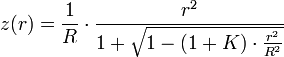
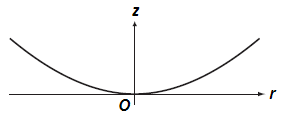
Suivant la valeur de conicité K, le profil prendra différentes formes :
K Profil K > 0 elliptique (grand axe // Or) K = 0 sphérique –1 < K < 0 elliptique (grand axe // Oz) K = –1 parabolique K < –1 hyperbolique - Portail de la physique
- Portail de l’astronomie
Catégories : Lentille | Optique appliquée à la photographie | Technique de l'observation astronomique
Wikimedia Foundation. 2010.
