- Lemme de Wirtinger
-
Inégalité de Wirtinger
En mathématiques et plus précisément en analyse, l'inégalité de Wirtinger compare la valeur moyenne du carré d'une fonction continument dérivable avec la moyenne du carré de sa dérivée.
Elle est utilisée en géométrie, par exemple pour établir un théorème isopérimétrique, elle est aussi utilisée dans la théorie des séries de Fourier. Intuitivement, la dérivation amplifie les différents termes du spectre en fréquence, et ce d'autant plus qu'ils sont d'ordre plus élevé. Donc l'énergie totale du signal dérivé est plus forte que celle du signal initial.
Sommaire
Énoncé
Soit f une fonction définie sur un intervalle [a, b], où a et b sont deux nombres réels tel que a est plus strictement petit que b. La fonction f est continue et de classe C1 par morceaux.
-
- Si l'intégrale de f entre a et b est nulle, la majoration suivante, dite inégalité de Wirtinger est vérifiée :
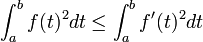
Cas d'égalité
Le seul cas d'égalité est celui où il existe deux nombres réels α et β tels que :
![\forall t \in [a,b] \quad f(t)=\alpha \cos(\omega t)+\beta \sin(\omega t) \quad\text{avec}\quad \omega = \frac {2\pi}{b-a}](/pictures/frwiki/51/364384670292d7f9147f03b5c836946f.png)
Démonstrations
Il existe de nombreuses manières de démontrer ce résultat ; la plus simple utilise la théorie des séries de Fourier[1]. Quitte à effectuer un changement de variable affine convenable, on peut limiter la démonstration au cas a = 0 et b = 2π. La fonction f est continue sur [0, 2π] et son carré est intégrable. Au sens de L2, qui désigne ici le Hilbert des fonctions définies sur [0, 2π], à valeurs réelles et de carrés sommables, on dispose de l'égalité suivante :

L'égalité de Parseval indique que :
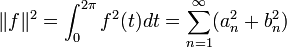
On remarque l'absence de constante a0 dans les deux formules précédentes. Cette absence est la conséquence du fait que l'intégrale de f entre 0 et 2π est nulle.
Si la dérivée de f n'est pas de carré intégrable, cela signifie que la valeur de l'intégrale est infinie et l'inégalité est vérifiée. Dans le cas contraire, le développement en série de Fourier de la dérivée est égal à :
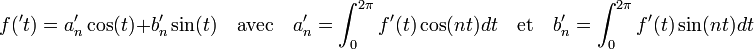
Une intégration par parties montre que :
![a'_n = \int_0^{2\pi}f'(t)\cos (nt)dt = \Big[f(t)\cos (nt)\Big]_0^{2\pi} + n\int_0^{2\pi}f(t)\sin (nt)dt = nb_n](/pictures/frwiki/48/0eb2804fab4a3702727479303dad14a4.png)
On montre de même que b'n est égal à -n.an, ce qui permet de déduire, à partir de l'égalité de Parseval :
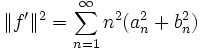
L'égalité est toujours stricte, sauf si an et bn sont nuls chaque fois que n est différent de 1.
Voir aussi
Notes
- ↑ C'est par exemple le choix de : Marcel Berger, Bernard Gostiaux, Géométrie différentielle : variétés, courbes et surfaces [détail des éditions] p 345
Liens externes
- (en) Wirtinger's inequality Planetmath.org
- (fr) P. Pansu Superrigidité géométrique et applications harmoniques Univ Paris-Sud, Laboratoire de Mathématiques d’Orsay
Références
Marcel Berger, Bernard Gostiaux, Géométrie différentielle : variétés, courbes et surfaces [détail des éditions]
- Portail des mathématiques
Catégories : Inégalité | Théorème de mathématiques -
Wikimedia Foundation. 2010.
