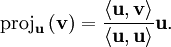Lemme d'orthonormation

Lemme d'orthonormation

Procédé de Gram-Schmidt

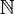En algèbre linéaire, dans un espace vectoriel muni d'un produit scalaire, le procédé de Gram-Schmidt[1], en notant N= [0,p]\, ou \mathbb N\, est un algorithme pour construire de proche en proche une base orthonormée à partir d'une base donnée.

Précisément :

Théorème — Si 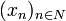(x_n)_{n \in N}\, est une famille libre d'un espace préhilbertien, il existe une et une seule famille orthonormée 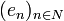(e_n)_{n \in N}\, telle que :

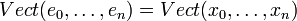  • Vect(e_0, \ldots, e_n) = Vect(x_0, \ldots, x_n)\, pour tout n\,
  • le produit scalaire 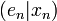(e_n|x_n)\, est strictement positif

On oublie souvent la condition d'unicité. Elle permet de parler de l 'orthonormalisée de Gram-Schmidt.

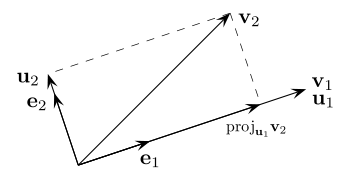
L'étape générale de l'algorithme consiste à soustraire au vecteur vj + 1 sa projection orthogonale sur l'espace Fj. On s'appuie sur la famille orthonormale déjà construite pour le calcul de projection.

Cette méthode a été nommée en hommage à Jørgen Pedersen Gram et Erhard Schmidt, mais elle est plus ancienne et est retrouvée dans des travaux de Laplace et Cauchy.

Applications.

  • Le procédé d'orthonormalisation de Gram-Schmidt donne (constructivement !) l'existence de bases orthonormées pour tout espace euclidien ou hermitien.
  • On peut aussi orthonormaliser la base canonique (1,X,...)de R[X] et obtenir ainsi une famille de polynômes orthogonaux.


Procédé de Gram-Schmidt

Nous définissons l'opérateur de projection sur une droite vectorielle par :

\mathrm{proj}_{\mathbf{u}}\,(\mathbf{v}) = {\langle \mathbf{u}, \mathbf{v}\rangle\over\langle \mathbf{u}, \mathbf{u}\rangle}\mathbf{u}.

Le procédé de Gram-Schmidt est alors :

Les deux premières étapes du procédé de Gram–Schmidt.
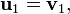
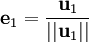
\mathbf{u}_1 = \mathbf{v}_1, \mathbf{e}_1 = {\mathbf{u}_1 \over ||\mathbf{u}_1||}
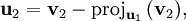
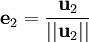
\mathbf{u}_2 = \mathbf{v}_2-\mathrm{proj}_{\mathbf{u}_1}\,(\mathbf{v}_2), \mathbf{e}_2 = {\mathbf{u}_2 \over ||\mathbf{u}_2||}
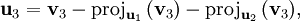
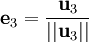
\mathbf{u}_3 = \mathbf{v}_3-\mathrm{proj}_{\mathbf{u}_1}\,(\mathbf{v}_3)-\mathrm{proj}_{\mathbf{u}_2}\,(\mathbf{v}_3), \mathbf{e}_3 = {\mathbf{u}_3 \over ||\mathbf{u}_3||}
\vdots \vdots
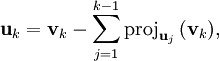
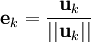
\mathbf{u}_k = \mathbf{v}_k-\sum_{j=1}^{k-1}\mathrm{proj}_{\mathbf{u}_j}\,(\mathbf{v}_k), \mathbf{e}_k = {\mathbf{u}_k\over||\mathbf{u}_k||}

Notes et références

  1. ↑ Mathématiques Tout-en-un . 2e année MP, Dunod, 2004, 2e éd. (ISBN 2-10-007576-4), p. 569 
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Proc%C3%A9d%C3%A9 de Gram-Schmidt ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Lemme d'orthonormation de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Lemme d'orthonormation de Gram-Schmidt — Procédé de Gram Schmidt En algèbre linéaire, dans un espace vectoriel muni d un produit scalaire, le procédé de Gram Schmidt[1], en notant ou est un algorithme pour construire de proche en proche une base orthonormée à partir d une base donnée.… …   Wikipédia en Français

  • Erhard Schmidt — Pour les articles homonymes, voir Schmidt. Erhard Schmidt Erhard Schmidt (13 janvier 1876 6 décemb …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”