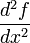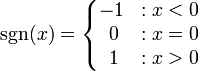Le test de la dérivée seconde
- Le test de la dérivée seconde
-
Dérivée seconde
La dérivée seconde est la dérivée de la dérivée d'une fonction, lorsqu'elle est définie.
Fonction d'une seule variable réelle
Si la fonction admet une dérivée seconde et que cette dérivée seconde est continue, la fonction est dite de classe C2.
Notation
Si on note ƒ(x) la fonction, alors
- la dérivée est notée ƒ '(x) ou
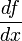 , et
, et
- la dérivée seconde est notée ƒ ''(x) (« f seconde de x ») ou
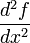
La dérivée seconde indique la variation de la pente :
- si elle est positive sur un intervalle, la pente augmente, la courbure est vers le haut, la fonction est dite « convexe » sur cet intervalle ;
- si elle est négative sur un intervalle, la pente diminue, la courbure est vers le bas, la fonction est dite « concave » sur cet intervalle ;
- si elle est nulle, la courbe est localement rectiligne ;
- si la dérivée seconde s'annule et change de signe, on a un point d'inflexion, la courbure de la courbe s'inverse.
Fonction n'admettant pas de dérivée seconde
- Les fonctions non dérivables en un point n'y admettent pas de dérivée seconde ; a fortiori les fonctions non continues en un point ;
- une primitive d'une fonction continue non dérivable est une fonction continue et dérivable, mais elle n'a pas de dérivée seconde aux points où la fonction initiale n'est pas dérivable ; c'est notamment le cas de la primitive de primitive d'une fonction non continue mais bornée.
- une primitive double de la fonction signe, ∫∫sgn
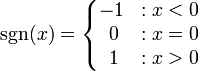
- une primitive double d'une fonction carrée, la primitive d'une fonction triangulaire (en dents de scie) ;
- une primitive double de la fonction partie entière ∫∫E(t)·dt;
- une primitive double de la fonction partie décimale ∫∫(x-E(t))·dt ;
La primitive seconde d'une fonction en dents de scie est dérivable une fois mais pas deux
|
La primitive seconde de la fonction partie décimale est dérivable une fois mais pas deux
|
La primitive seconde de la partie entière est dérivable une fois mais pas deux
|
Voir aussi
Catégories : Mathématiques élémentaires | Analyse réelle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Le test de la dérivée seconde de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Derivee — Dérivée Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… … Wikipédia en Français
Dérivée (mathématiques élémentaires) — Dérivée Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… … Wikipédia en Français
Dérivée première — Dérivée Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… … Wikipédia en Français
Dérivée — En analyse, le nombre dérivé en un point d une fonction à variable et valeurs réelles est le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est le coefficient directeur de l approximation affine de cette fonction… … Wikipédia en Français
Dérivable — Dérivée Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… … Wikipédia en Français
Dérivation (mathématiques élémentaires) — Dérivée Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… … Wikipédia en Français
Dérivées — Dérivée Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… … Wikipédia en Français
Nombre dérivé — Dérivée Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… … Wikipédia en Français
Taux d'accroissement — Dérivée Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
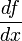 , et
, et