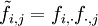Analyse Factorielle Des Correspondances

Analyse factorielle des correspondances

Pour les articles homonymes, voir AFC.

L'analyse factorielle des correspondances, en abrégée AFC, est une méthode statistique d'analyse des données mise au point par Jean-Paul Benzecri à l'Université Pierre-et-Marie-Curie à Paris (ISUP et Laboratoire de statistique multidimensionnelle)

Introduction

Dit grossièrement, une méthode AFC admet en entrée un "tableau croisé dynamique" comme sous Excel, et produit en sortie une ou plusieurs cartes ou images de répartition des valeurs et des variables. Exemple : La participation croisée boursière; si 6 investisseurs répartissent leurs portefeuille entre 10 entreprises, on obtient par AFC une carte comprenant 16 points, dont 6 représentent chacun des investisseurs et les 10 autres représentent chacune des 10 entreprises. l'analyse apporte en fait l'information de distance entre les points permettant d'interpréter indirectement les pourcentages de participation au capital des entreprises.

La technique de l'AFC est essentiellement utilisée pour de grands tableaux de données toutes comparables entre elles (si possible exprimées toutes dans la même unité, comme une monnaie, une dimension, une fréquence ou toute autre grandeur mesurable). Elle peut en particulier permettre d'étudier des tableaux de contingence (ou tableau croisé de co-occurrence). De manière générale, les méthodes factorielles permettent l'analyse d'un tableau "agrégé" de mesures, correspondant aux requêtes du type "select count(*) from .. group by (tuple_dimensions)" en langage SQL ou aux tableaux croisés dynamiques sous Excel, tandis que les méthodes d'exploration de données travaillent directement sur les mesures récoltées pour chaque individu. Ces méthodes-là sont donc particulièrement recommandées pour les analyses de rapports d'études.

l'AFC sert à déterminer et à hiérarchiser toutes les dépendances entre les lignes et les colonnes du tableau.

Le principe de ces méthodes est de partir sans a priori sur les données et de les décrire en analysant la hiérarchisation de l'information présente dans les données. Pour ce faire, les analyses factorielles étudient l'inertie du nuage de points ayant pour coordonnées les valeurs présentes sur les lignes du tableau de données.

La "morphologie du nuage" et la répartition des points sur chacun de ces axes d'inertie permettent alors, de rendre lisible et hiérarchisée l'information contenue dans le tableau. Mathématiquement, après avoir centré et réduit le tableau de données que l'on a affecté d'un système de masse (par exemple, les sommes marginales de chaque ligne), on calcule la matrice d'inertie associée et on la diagonalise (la répartition de l'information selon les différents axes est représentée par l'histogramme des valeurs propres). On effectue alors un changement de base selon ses vecteurs propres, c'est-à-dire selon les axes principaux d'inertie du nuage de points. On projette alors les points figurant chaque ligne sur les nouveaux axes. L'ensemble de l'information est conservée, mais celle-ci est maintenant hiérarchisée, axe d'inertie par axe d'inertie. L'histogramme des valeurs propres permet de voir le type de répartition de l'information entre les différents axes et l'étendue en dimension de celle-ci.

Le premier axe d'inertie oppose les points, c'est-à-dire les lignes du tableau ayant les plus grandes distances ou "différences". La première valeur propre d'inertie, (associée à ce premier axe) mesure la quantité d'information présente le long de cet axe, c'est-à-dire dans cette opposition. On analyse ainsi les différents axes, en reconstituant progressivement la totalité des données.

Plusieurs méthodes d'analyse des correspondances existent, qui diffèrent par le type de représentation de l'information, c'est-à-dire de métrique, ou de système de masse qu'elles utilisent.

L'analyse factorielle des correspondances AFC développée par Jean-Paul Benzecri et ses collaborateurs emploie la métrique du chi-deux : chaque ligne est affectée d'une masse qui est sa somme marginale, le tableau étudié est le tableau des profils des lignes, ce qui permet de représenter dans le même espace à la fois les deux nuages de points associés aux lignes et aux colonnes du tableau de données ; elle est par ailleurs très agréablement complétée par des outils de classification ascendante hiérarchique (CAH) qui permettent d'apporter des visions complémentaires, en particulier en construisant des arbres de classification des lignes ou des colonnes.

Pour chaque point représentatif des lignes ou des colonnes du tableau de données, nouvel axe par nouvel axe, on s'intéresse à ses nouvelles coordonnées, au cosinus carré de l'angle avec l'axe (ce qui est équivalent à un coefficient de corrélation), ainsi qu'à sa contribution à l'inertie expliquée par l'axe (c'est-à-dire à sa contribution à la création de l'axe).

Deux contraintes particulières sur les données sont à signaler : d'une part, les tableaux ne peuvent comporter de cases vides et d'autre part, seules des valeurs positives sont permises. De plus, compte tenu de la métrique du chi-deux employée par l'AFC, cette méthode accorde une importance plus grande aux lignes de somme marginale élevée. Si nous utilisons des tableaux quantitatifs et souhaitons équilibrer la contribution de chaque ligne au calcul de l'inertie, nous devons transformer le tableau pour assurer à chaque ligne une somme marginale égale. Pour ce faire, on peut dédoubler chaque ligne, en lui adjoignant un tableau de complément. A chaque valeur fij, on fait correspondre une valeur dédoublée k-fij, avec k>=max(fij).

Par l'AFC, il est tout autant possible d'analyser des tableaux contenant des mesures quantitatives que des indications qualitatives, (par exemple une donnée "couleur"), ces deux types ne pouvant être mélangés. Un cas particulier de la deuxième catégorie de tableau est constituée par les tableaux "disjonctifs" ; plusieurs variables constituent les colonnes : elles sont toutes découpées en plusieurs modalités, dont une et une seule est vraie par individu. Lors d'une analyse factorielle, on peut rajouter des données "supplémentaires", c'est-à-dire que l'on ne fait pas intervenir dans le calcul de l'inertie, mais que l'on projette sur les axes.

Exemple d'application

Par exemple, on a demandé à un ensemble d'électeurs leur département et leur vote à l’élection présidentielle. Il est commode de regrouper ces données dans un tableau de contingence. Supposons qu'il y a I candidats et J départements :

$M=\begin{bmatrix} n_{1,1} & n_{1,2} & \cdots & n_{1,J}\\ n_{2,1} & n_{2,2} & \cdots & n_{2,J}\\ \vdots & \vdots & \ddots & \vdots\\ n_{I,1} & n_{I,2} & \cdots & n_{I,J}\\ \end{bmatrix}$

n i, j

représente le nombre de personnes ayant voté pour le candidat i dans le departement j.

Fréquemment, on utilise la fréquence remplaçant le nombre de personnes.

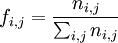$f_{i,j}=\frac{n_{i,j}}{\sum_{i,j} n_{i,j}}$ ,

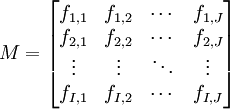
$M=\begin{bmatrix} f_{1,1} & f_{1,2} & \cdots & f_{1,J}\\ f_{2,1} & f_{2,2} & \cdots & f_{2,J}\\ \vdots & \vdots & \ddots & \vdots\\ f_{I,1} & f_{I,2} & \cdots & f_{I,J}\\ \end{bmatrix}$

On note

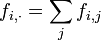$f_{i,\cdot}=\sum_{j} f_{i,j}$ ,

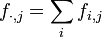$f_{\cdot,j}=\sum_{i} f_{i,j}$ ,

respectivement les profils-lignes et les profils-colonnes.

Un tel tableau est constitué dans la perspective de l'étude de la liaison entre deux variables catégorielles: Quels sont les candidats "préférés" dans un département ?

La distance $χ 2$

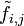
Etudier la liaison entre deux variables qualitatives revient à étudier l'écart entre les données observées et une situation théorique d'indépendance. Cette situation théorique correspond au tableau : $\tilde{f}_{i,j}$

$\tilde{f}_{i,j}=f_{i,\cdot}f_{\cdot,j}$

Si le tableau des données vérifie la relation d'indépendance 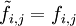$\tilde{f}_{i,j}=f_{i,j}$ , alors tous les profils-lignes d'une part et tous les profils-colonnes d'autre part sont égaux au profil moyen correspondant.

L'écart à l'indépendance est pris en compte en considérant le tableau X de terme général:

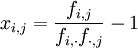$x_{i,j}=\frac{f_{i,j}}{f_{i,\cdot}f_{\cdot,j}}-1$ ,

On peut tester l'hypothèse d'indépendance par le test $χ 2$ (prononcé "Ki-2")

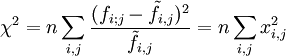$\chi^2=n\sum_{i,j}\frac{(f_{i;j}-\tilde{f}_{i,j})^2}{\tilde{f}_{i,j}}=n\sum_{i,j}x_{i,j}^2$ ,

Cette statistique vaut 0 ou proche 0 si les données observées vérifient le modèle d'indépendance. Mais cette statisque ne répond pas aux questions suivantes:

Par case: quelles sont, entre une modalité ligne i et une modalité colonne j, les associations les plus remarquables?
Par ligne: quelles sont les départements qui ont un profil de vote particulier?
Par colonne: quels sont les candidats qui ont un électorat particulier?

Pour répondre à ces questions, on rappelle que l'analyse en composantes principales (ACP) peut réduire la dimension des problèmes et sélectionner les effets principaux. Mais une métrique spéciale est adaptée-la métrique du $χ 2$ . Dans ce sens, l'AFC peut être considérée comme une ACP particulière dotée de la métrique du $χ 2$ qui ne dépend que du profil des colonnes du tableau.

Considérons le tableau X, chaque ligne peut être considéré comme un point dans l'espace de dimension J, noté 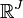$\Bbb{R}^J$ , dont chaque dimension est associée à une colonne du tableau X. On affecte à la ligne i un poids proportionnel à son effectif soit 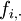$f_{i,\cdot}$ . Le centre de gravité est confondu avec l'origine des axes :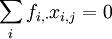

$\sum_{i}f_{i,\cdot}x_{i,j}=0$

La distance $χ 2$ est définie comme (to be continued)

Extension

La technique de l'AFC peut être utilisée pour des tableaux d'un autre type que tableau de contingence. En revanche, son utilisation pour ces tableaux oblige toujours à des adaptations spécifiques au type de tableau. On peut utiliser l'AFC sur des tableaux :

logiques
logiques dédoublés
de notes d'intensité
de rang
de mesure
qualitatifs

Lorsque l'on utilise l'AFC sur des tableaux disjonctifs complet ou de Burt , on utilise en réalité la méthode de l'analyse des correspondantes multiples (ACM).

Bibliographie

Histoire et préhistoire de l'analyse des données, Dunod, 1982, ISBN 2-04-015467-1
L'analyse des données / lecons sur l'analyse factorielle et la reconnaissance des formes et travaux, Dunod 1982, ISBN 2-04-015515-5
Linguistique et lexicologie, Dunod, 2007 réédition, ISBN 2-04-010776-2
Pratique de l'analyse des données, Dunod, 1980, ISBN 2-04-015732-8

Michel Volle, Analyse des données, Economica, 4^e édition, 1997, ISBN 2-7178-3212-2

Le Roux B. et Rouanet H., Geometric Data Analysis, Kluwer Academic Publishers, Dordrecht (June 2004)

Voir aussi

Liens externes

Cours d'Analyse factorielle des Correspondances (il s'agit d'un cours de base, pas à pas, intitulé « l'AFC pour les nuls »)
Principe de l'analyse factorielle par le Pr Philippe Cibois, auteur des "Que sais-je" sur le sujet - le site contient également un logiciel libre de dépouillement d'enquête, Trideux
FactoMineR, une bibliothèque de fonctions R dédiée à l'analyse des données
CARME-N, une autre bibliothèque d'analyse factorielle pour le langage R
SPAD, Logiciel spécialisé dans les analyses multivariées et les classifications
STATGRAPHICS et son module UNIWIN Plus
IMSL, une bibliothèque mathématique et statistique pour C/C++, C#, Java, Fortran et Python
Exemple d'application : le moteur cartographique Kartoo
Différents critères d'optimisation de l'inertie dans les méthodes factorielles : equamax, varimax et quartimax (en anglais)

Ce document provient de « Analyse factorielle des correspondances ».

Catégories : Analyse des données | Méthode d'analyse

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Analyse Factorielle Des Correspondances de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Analyse factorielle des correspondances — ● Analyse factorielle des correspondances méthode d analyse des données visant à décrire au mieux les proximités entre des individus sur lesquels sont observées les modalités de deux caractères qualitatifs … Encyclopédie Universelle
Analyse factorielle des correspondances — Pour les articles homonymes, voir AFC. L analyse factorielle des correspondances, en abrégée AFC, est une méthode statistique d analyse des données mise au point par Jean Paul Benzecri à l Université Pierre et Marie Curie à Paris (ISUP et… … Wikipédia en Français
Analyse factorielle — L analyse factorielle est une méthode de la famille de la statistique multivariée, utilisée pour décrire la variabilité entre des variables observées, au moyen de variables latentes (non observées). Pour réduire le nombre de variables, la méthode … Wikipédia en Français
Analyse des correspondances multiples — Pour les articles homonymes, voir ACM. L Analyse des correspondances multiples, en abrégée ACM, est une méthode statistique d analyse des données ; il s agit d une extension de l analyse factorielle des correspondances. L ACM peut être menée … Wikipédia en Français
Analyse canonique des corrélations — L Analyse canonique des corrélations[i 1] permet de comparer deux groupes de variables quantitatives appliqués tous deux sur les mêmes individus. Le but de l analyse canonique est de comparer ces deux groupes de variables pour savoir si ils… … Wikipédia en Français
Analyse des correspondantes multiples — Analyse factorielle des correspondances Pour les articles homonymes, voir AFC. L analyse factorielle des correspondances, en abrégée AFC, est une méthode statistique d analyse des données mise au point par Jean Paul Benzecri à l Université Pierre … Wikipédia en Français
Analyse confirmative de données — Analyse des données L’analyse des données est un sous domaine des statistiques qui se préoccupe de la description de données conjointes. On cherche par ces méthodes à donner les liens pouvant exister entre les différentes données et à en tirer… … Wikipédia en Français
Analyse de données — Analyse des données L’analyse des données est un sous domaine des statistiques qui se préoccupe de la description de données conjointes. On cherche par ces méthodes à donner les liens pouvant exister entre les différentes données et à en tirer… … Wikipédia en Français
Analyse des données (statistiques) — Analyse des données L’analyse des données est un sous domaine des statistiques qui se préoccupe de la description de données conjointes. On cherche par ces méthodes à donner les liens pouvant exister entre les différentes données et à en tirer… … Wikipédia en Français
Analyse exploratoire de données — Analyse des données L’analyse des données est un sous domaine des statistiques qui se préoccupe de la description de données conjointes. On cherche par ces méthodes à donner les liens pouvant exister entre les différentes données et à en tirer… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Analyse Factorielle Des Correspondances