- Lame de Schmidt
-
La lame de Schmidt, inventée par Bernhard Schmidt en 1930[1], est une lentille utilisée pour corriger l'aberration géométrique dans les télescopes utilisant un miroir primaire sphérique et placée au rayon de courbure du miroir. Ceci est ce qui est généralement admis.
En fait l'idée d'utiliser une lame asphérique revient d'abord à G.A.H.Kellner (1907) qui la place non loin du miroir sphérique (Brevet US 969 785) dans le cadre d'une lanterne de projection et rate ainsi de peu la célébrité, puis à Vaïsala (1924) qui a montré des notes de cours comme preuve de sa revendication. Néanmoins à cette époque le besoin ne se faisait pas sentir d'un astrographe très ouvert et la réalisation de la lame semblait hors de porté. Le mérite de Schmidt tient moins dans la redécouverte de la lame qui porte son nom mais d'une part dans l'idée de la mettre au rayon de courbure et dans l'invention d'une méthode permettant "facilement" de la réaliser, la méthode par dépression et d'autre part dans la diffusion de son invention au bon moment.
Cette lame correctrice est placée à l'entrée du tube du télescope où elle forme la pupille d'entrée, au niveau du centre optique du miroir dans le cas d'une chambre de Schmidt ce qui a pour effet de supprimer la coma et l'astigmatisme, seul demeure la courbure de champ, ou juste derrière le foyer du miroir dans le cas d'un télescope de type Schmidt-Cassegrain.
La géométrie de la lame de Kellner-Schmidt, plus épaisse au milieu et sur les bords, permet de corriger le chemin optique parcouru par la lumière afin de faire en sorte que les rayons se réfléchissant sur les bords externes du miroir se focalisent au même endroit que ceux qui se réfléchissent plus près du centre du miroir. Cette lentille ne participe qu'à la correction de l'aberration sphérique et ne change en rien la focale de l'instrument sur lequel elle est utilisée.
Anatomie de la lame de Schmidt
Schéma en coupe transversale d'une lame de Schmidt
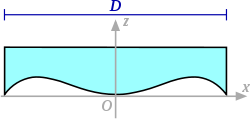
La lame de Schmidt possède d'un côté une face plane, et de l'autre une face obéissant à l'équation suivante :
Cette formule est valable dans un repère orthonormé direct, l'axe Oz étant normal à la surface plane de la lame et l'origine O se trouvant sur le ventre de cette dernière. La formule adopte les conventions suivantes :
- D est le diamètre de la lame
- Rc est le rayon de courbure du miroir sphérique associé
- n est l'indice de réfraction du verre dans lequel est taillée la lame
- k est un paramètre permettant de définir la forme exacte de la lame
L'aberration chromatique minimale est obtenue pour k = 1,5 [2].
Principe d'utilisation
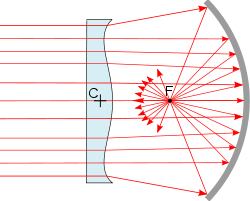
Trajets lumineux dans un cas de correction par une lame de SchmidtLa lame de Kellner-Schmidt corrige la trajectoire des rayons incidents, favorisant ainsi le convergence au foyer du miroir. Cette correction a son maximum d'efficacité pour les rayons provenant de l'infini et parallèles à l'axe optique. Utilisée en combinaison avec un miroir sphérique (cas d'un télescope de type Schmidt-Cassegrain), elle permet d'obtenir un instrument moins sensible à l'obliquité des rayons que ne le serait un instrument à miroir parabolique.
Il est à noter que la correction aberration sphérique effectuée par la lame ne corrige pas la courbure du champ.
Notes
Wikimedia Foundation. 2010.
